目录




椭圆抛物面的标准方程

性质





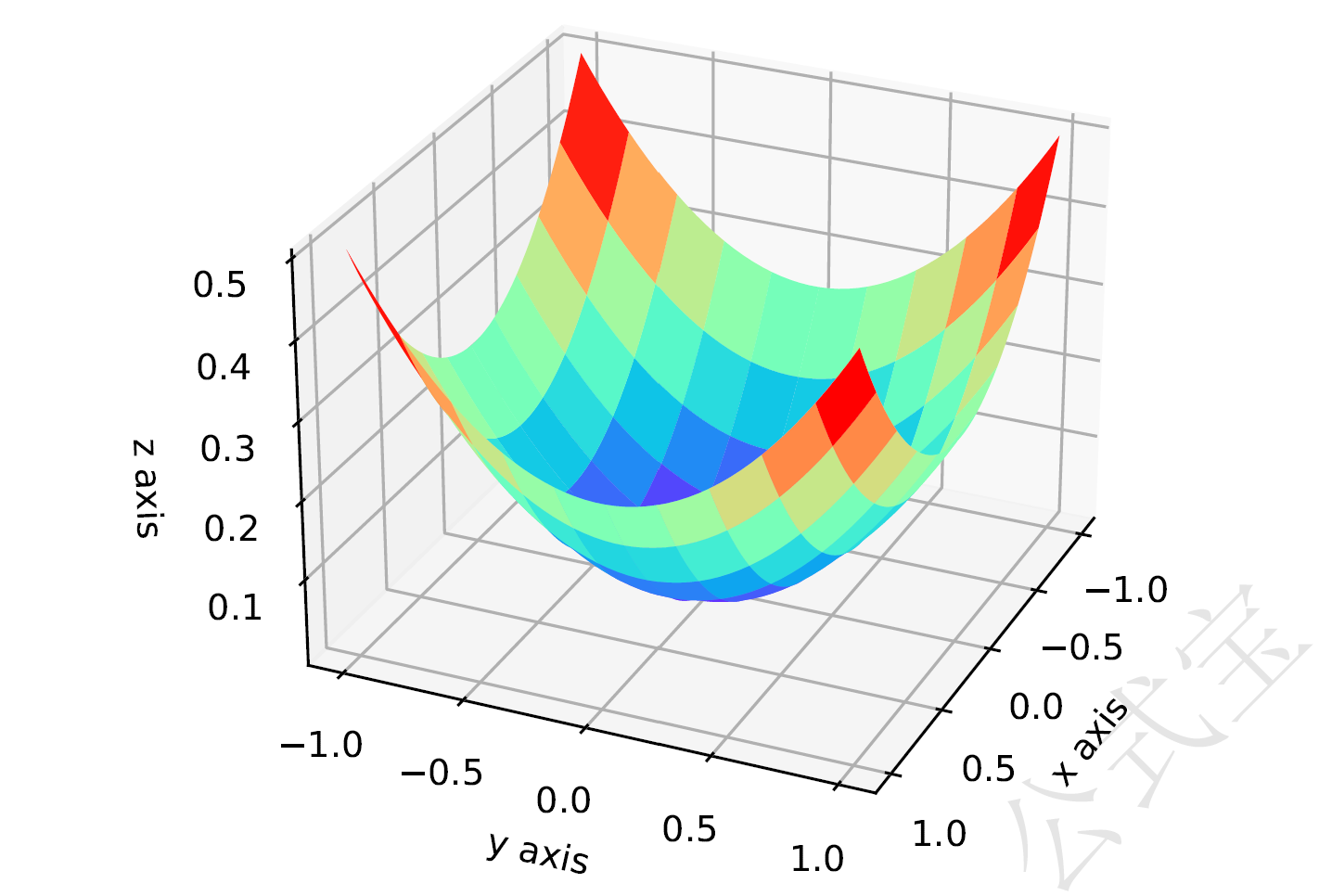
椭圆抛物面的标准方程
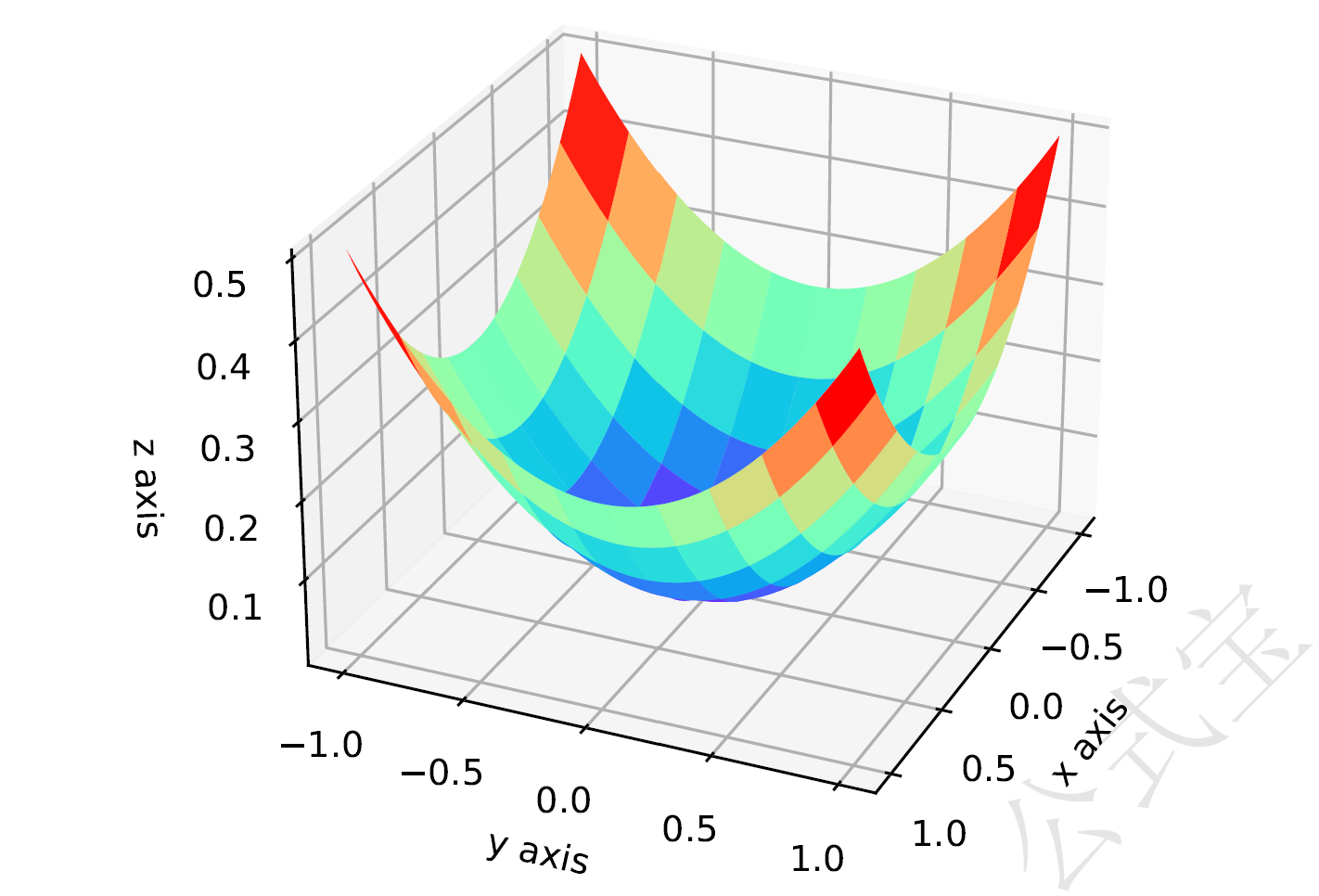
性质




