一般地,函数$$y=a^{x}(a>0,且a\neq 1)$$叫作指数函数,其中$x$是自变量,函数的定义域是$R$。
因为$a>0,x$是任意一个实数,$a^{x}$是一个确定的实数,所以函数的定义域为实数集$R$。
规定底数$a$大于零且不等于$1$的理由:
如果$a=0$,当 $$\begin{cases} x>0& 时,\text a^{x}恒等于0;\\ x\leqslant0&时,\text a^{x}无意义。 \end{cases}$$
如果$a<0$,比如 $y =(-4) ^{x}$,这时对于 $$x =\frac{1}{4}, x= \frac{1}{2}, \cdots, $$ 在实数范围内函数值不存在。
如果$a=1$,$$y=1^{x}=1,$$是一个常量对它就没有研究的必要。
为了避免上述各种情况,所以规定$$a>0,且a\neq 1.$$
像$$y=2 \cdot 3^{x},y=3^{\frac{1}{x}},y=3^{\sqrt {x+2}},y=3^{x}+1$$等函数都不是指数函数,要注意区分开。
正整数指数幂
$$a^{n}=\underbrace{a\cdot a \cdots a}_{n个}(n\in N^{*});$$
零指数幂
$$a^{0}=1(a\neq0);$$
负整数指数幂
$$a^{-n}={1 \over a^{n}}(a\not =0,n\in N^{*});$$
正分数指数幂
$$a^{{m \over n}}=\sqrt[n]{a^{m}}(a>0,m,n\in N^{*}且n > 1)。$$
负分数指数幂
$$a^{-\frac{m}{n}}=\frac{1}{a^{\frac{m}{n}}}=\frac{1}{\sqrt[n]{a^{m}}}(a>0,m,n \in N^{*}且 n > 1)。$$
同底数的幂相乘
同底数的幂相乘,底数不变,指数相加。$$\\a^{r} a^{s} =a^{r+s} (a>0,r,s\in Q)$$
幂的乘方
幂的乘方,底数不变,幂指数与乘方次数相乘。$$\\(a^{r})^{s} =a^{rs} (a>0,r,s\in Q)$$
积的乘方
积的乘方,各因式分别乘方再相乘。$$\\(ab)^{r}=a^{r} b^{r} (a>0,b>0,r\in Q)$$
分式乘方
分式乘方,分子乘方所得的幂作分子,分母乘方所得的幂作分母。$$\\(\frac{a}{b})^{\alpha}=\frac{a^ {\alpha}}{b^ {\alpha}} (a>0,b>0,\alpha \in Q)$$
对有理数指数幂运算法则中$"a>0,b>0"$的理解
运用有理数指数幂运算法则进行运算时,必须注意幂的底数是正数的规定,如若改变等式成立的条件,则命题就有可能不成立,
如$$a=-2,b=-3,\alpha=\frac{1}{4},$$则$$ (ab)^ {\alpha}=[(-2) (-3)]^{\frac{1}{4}}=6^{\frac{1}{4}},$$而$$(-2)^{\frac{1}{4}},(-3)^{\frac{1}{4}}$$都无意义, 所以当 $a<0,b<0$时,有理数的运算性质$$(ab)^{r}=a^{r} b^{r} (r\in Q) $$就不成立了。
根式与分数指数幂的实质是相同的,分数指数幂与根式可以相互转化,通常利用分数指数幂进行根式的简化运算。
一般地,无理数指数幂$$a^{\alpha}(a>0,\alpha是无理数)$$是一个确定的实数,如$$3^{\sqrt{3}},7^{\sqrt{2}}$$都是无理数指数幂,有理数指数幂的性质同样适用于无理数指数幂。
$0$的正分数指数幂等于$0$,$0$的负分数幂没有意义。
指数函数的单调性是由底数$a$的大小决定的,因此解题时通常对底数$a$按:$0 < a < 1$和$a > 1$进行分类讨论。
画指数函数$$y=a^{x} (a>0,且a \neq 1)$$的图像,应抓住三个关键点:$$(1,a),(0,1),(-1,\frac{1}{a}).$$
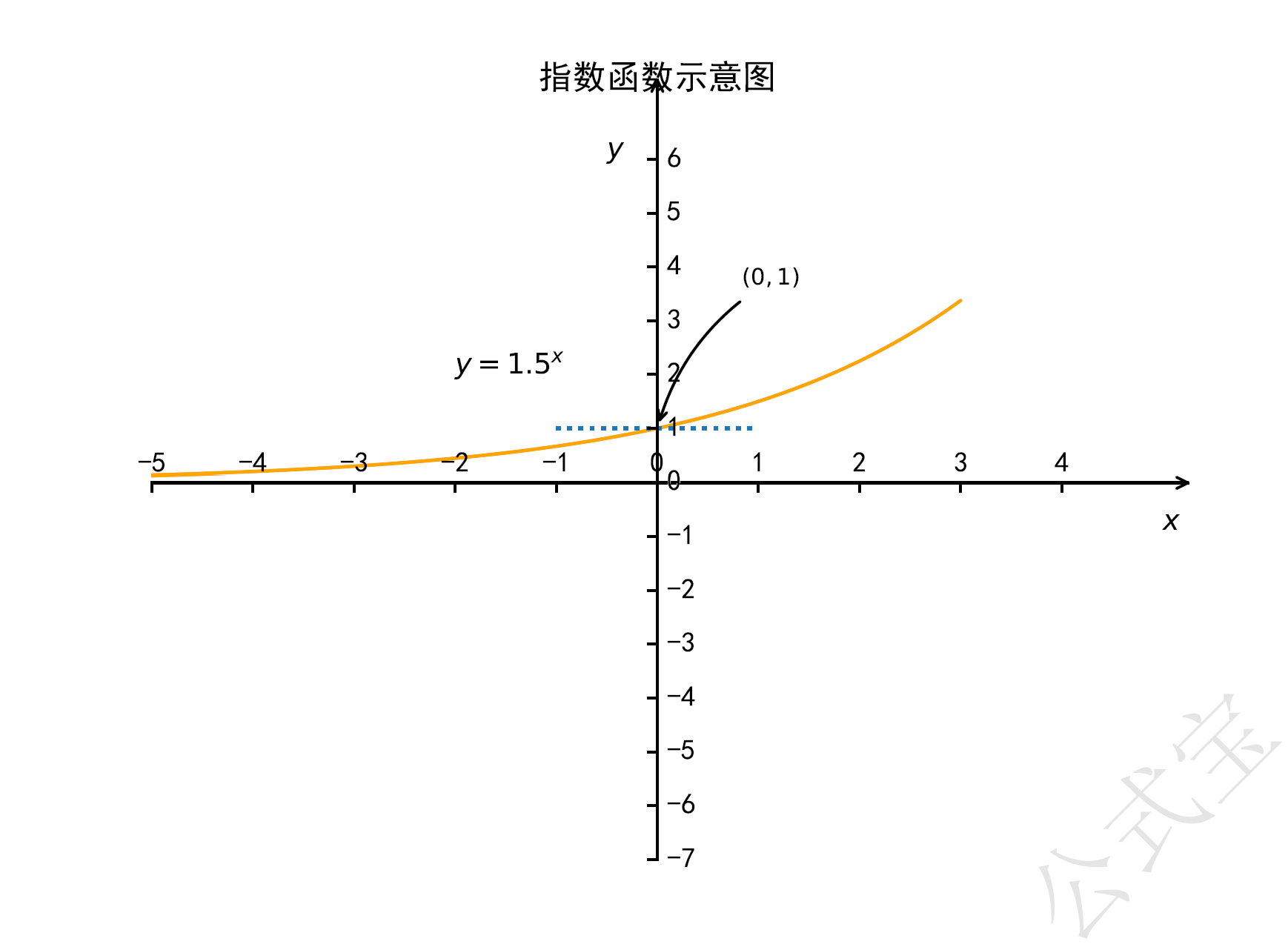
如图,函数$y=a^{x}$其性质有:过定点$(0,1)$,即$x=0$时,$y=1$。
当$$0 < a < 1$$时,$y=a^{x}$在$R$上是减函数,
当$$a > 1$$时,$y=a^{x}$在$R$上是增函数。

指数函数
指数函数
函数$$y=a^{x}(a>0,且a\neq 1)$$的图像与$$y=(\frac{1}{a})^{x}$$的图像关于$y$轴对称,
即底数互为倒数的两个指数函数的图像关于$y$对称。
在同一坐标系中,多个指数函数底数的变化规律是:如图,在第一象限内,$$a > 1$$时,底数越大,指数函数$y=a^{x}$的图像越靠近$y$轴;$$0 < a <1 $$时,底数越小,指数函数$y=a^{x}$的图像越接近$y$轴。

指数函数图像间的关系












