并联是元件之间的一种连接方式,其特点是将2个同类或不同类的元件、器件等首首相接,同时尾尾亦相连的一种连接方式。通常是用来指电路中电子元件的连接方式,即并联电路。
电阻并联
线性时不变电阻元件并联时,并联组合等效于一个电阻元件,其电导 (电阻的倒数) 等于各并联电阻的电导之和,称为并联 组合的等效电导,其倒数称为等效电阻。设电阻器1、2、3的电阻分别是 $R_1 、 R_2 、 R_3$ ,它们的电导分别是 $G_1 、 G_2 、 G_3$ 。则并联 电路的总电阻 $R$ 和总电导G按下面的公式计算:
$$\begin{aligned}& \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \\& G=G_1+G_2+G_3\end{aligned}$$
电容并联
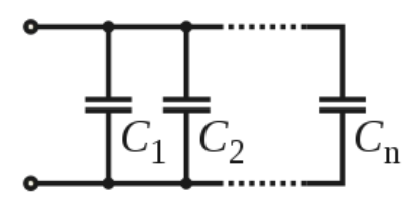
电容并联
如上图所示, $n$ 个电容器并联在一起。现将电源连接于这并联电路的两端。从电容的 定义,可以得到,通过第 $\mathrm{k}$ 个电容器的电流 $\mathrm{i} \mathrm{k}$ 等于其电容 $\mathrm{C}_{\mathrm{k}}$ 乘以其两端的电压改变率 $\frac{d v_k}{d t}$
$$i_k=C_k \frac{d v_k}{d t}$$
按照基尔霍夫电压定律,电源两端的电压等于每一个电容器两端的电压:
$$v=v_1=v_2=\cdots=v_n$$
根据基尔霍夫电流定律,从电源 (直流电或交流电) 给出的电流等于通过每一个电容器的电流的代数和:
$$i=i_1+i_2+\cdots+i_n=\left(C_1+C_2+\cdots+C_n\right) \frac{d v}{d t}$$
所以, $n$ 个电容器并联的等效电容 $C_{e q}$ 为:
$$C_{e q}=C_1+C_2+\cdots+C_n$$
电感并联
$n$ 个无互感理想电感器并联在一起,类似前面所述方法,可以计算出其等效电感 $L_{e q}$ 为:
$$\frac{1}{L_{e q}}=\frac{1}{L_1}+\frac{1}{L_2}+\cdots+\frac{1}{L_n}$$
其中, $L_i$ 是第 $i$ 个电感器的电感。
由于电感器产生的磁场会与其邻近电感器的缠绕线圈发生耦合,很难噼免紧邻的电感器彼此互相影响。物理量互感M 能够给 出对于这影响的衡量。上述方程描述 $n$ 个电感器无互感并联的理想案例。
由电感分别为 $L_1 、 L_2$ ,互感为 $M$ 的两个电感器构成的并联电路,其等效互感 $L_{e q}$ 为:
- 假设两个电感器分别产生的磁场或磁通量,其方向相同,则称为“并联互助”,以方程表示,
$$L_{e q}=\frac{L_1 L_2-M^2}{L_1+L_2-2 M}$$
- 假设两个电感器分别产生的磁场或磁通量,其方向相反,则称为“并联互消”,以方程表示,
$$L_{e q}=\frac{L_1 L_2-M^2}{L_1+L_2+2 M}$$
对于具有三个或三个以上电感器的并联电路,必需考虑到每个电感器自己本身的自感和电感器与电感器之间的互感,这会使 得计算更加复杂。
开关并联
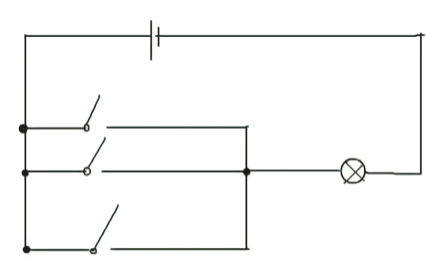
两个以上开关并联在一起,会形成逻辑“或电路”。假设连接电源于这电路的两端,则只要其中任意一个开关为闭合时,电流就会流通。
电源并联
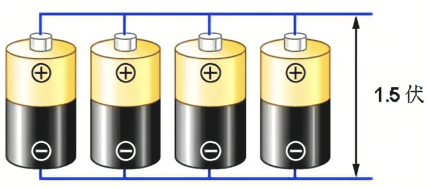
假设一个电池组是以几个电压相同的单电池以并联方式连接成电源,则此电源两端的电压等于每一个单电池两端的电压。例如,假设一个电池组内部含有四个单电池并联在一起,它们共同给出1安培电流,则每一个单电池给出0.25安培电流。很多年前,并联在一起的电池组时常会被使用为无线电接收机内部真空管灯丝的电源,但这种用法已不常见。
当电压不同的两个或更多电源并联连接时,由于有电势差的存在,电池组内部会形成电流回路,造成电能在电池组内部的消耗。
电流的特点
①在并联电路中干路电流等于各支路中电流之和。
②在并联电路中流过各支路的电流与其电阻成反比。
③在并联电路中,其中一个支路的电阻增大,该支路的电流减小,干路电流变小,而其他支路电流保持不变。
④在并联电路中某一个支路的电阻变小,该支路的电流变大.干路电流变大,而其他支路的电流保持不变。
⑤在并联电路中,各支路的电流互不影响。
电阻的特点
(1)在并联电路中总电阻的倒数等于各支路的电阻倒数之和。
(2)把n段导体并联起来,这相当于增大了导体的横截面积。所以,并联后的总组比任何一个分电阻都小。
(3) $n$ 个相同的电阻 $R_0$ ,并联,并联后的总电阻为 $R_{\text {总 }}=R_0 / n_{\text {。 }}$
(4)求两个电阻 $R_1 、 R_2$ 并联的总电阻 $R=R_1 R_2 /\left(R_1+R_2\right)$ ,(两电阻之积除除以两电阻之和。)
(5)在并联电路中,当并联的支路增加时,总电阻减小;干路的电流增大,而其他支路的电流保持不变。
6(6在并联电路中,某个支路的电阻减小,并联电路的总电阻减小;干路的电流增大,其它支路电流不变。
(7)在并联电路中,某个支路的电阻增大,并联电路的总电阻增大;干路的电流减小,其它支路电流不变。
电能的特点
①在并联电路中电路消耗的总电能等于各个用电器消耗的电能之和。
②在并联电路中各用电器消耗的电能与电阻成反比。
电功率的特点
①在并联电路中电路消耗的总功率等于各个用电器消耗的电功率之和。
②在并联电路中各用电器消耗的电功率与电阻成反比
电热的特点
①在并联电路中电路产生的总热量等于各用电器产生的热量之和。
②在并联电路中各用电器产生的热量与电阻成反比。
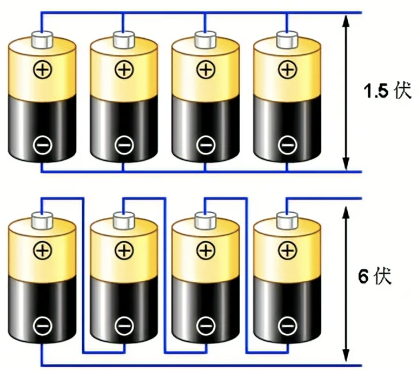
最直观的区别是这两种连接方式的电池所表现的不同特点,四节电池串联起来有6V,而并联则仍然只有1.5V。
1.串联电路
把元件逐个顺次连接起来组成的电路。如图2中的下图,特点是:流过一个元件的电流同时也流过另一个。例如:节日里的小彩灯。 在串联电路中,闭合开关,两只灯泡同时发光,断开开关两只灯泡都熄灭,说明串联电路中的开关可以控制所有的用电器。
2.并联电路
把元件并列地连接起来组成的电路,如上图,特点是:干路的电流在分支处分两部分,分别流过两个支路中的各个元件。例如:家庭中各种用电器的连接。 在并联电路中,干路上的开关闭合,各支路上的开关闭合,灯泡才会发光,干路上的开关断开,各支路上的开关都闭合,灯泡不会发光,说明干路上的开关可以控制整个电路,支路上的开关只能控制本支路。
3.串联电路和并联电路的特点
在串联电路中,由于电流的路径只有一条,所以,从电源正极流出的电流将依次逐个流过各个用电器,最后回到电源负极。因此在串联电路中,如果有一个用电器损坏或某一处断开,整个电路将变成断路,电路就会无电流,所有用电器都将停止工作,所以在串联电路中,各几个用电器互相牵连,要么全工作,要么全部停止工作。 在并联电路中,从电源正极流出的电流在分支处要分为两路,每一路都有电流流过,因此即使某一支路断开,但另一支路仍会与干路构成通路。由此可见,在并联电路中,各个支路之间互不牵连。
串联分压,并联分流
原理:在串联电路中,各电阻上的电流相等,各电阻两端的电压之和等于电路总电压。可知每个电阻上的电压小于电路总电压,故串联电阻分压。
在并联电路中,各电阻两端的电压相等,各电阻上的电流之和等于总电流(干路电流)。可知每个电阻上的电流小于总电流(干路电流),故并联电阻分流。 电阻的串并联就好像水流,串联只有一条道路,电阻越大,流的越慢,并联的支路越多,电流越大。
怎样判断电路中用电器之间是串联还是并联?
串联和并联是电路连接两种最基本的形式,它们之间有一定的区别。要判断电路中各元件之间是串联还是并联,就必须抓住它们的基本特征,具体方法是:
(1)用电器连接法:分析电路中用电器的连接方法,逐个顺次连接的是串联;并列在电路两点之间的是并联。
(2)电流流向法:当电流从电源正极流出,依次流过每个元件的则是串联;当在某处分开流过两个支路,最后又合到一起,则表明该电路为并联。
(3)去除元件法:任意拿掉一个用电器,看其他用电器是否正常工作,如果所有用电器都被拿掉过,而且其他用电器都可以继续工作,那么这几个用电器的连接关系是并联;否则为串联。
(4)用笔画线代替导线,能用一根导线将所有用电器连起来即为串联,不能则为并联。