目录




三角形的定义

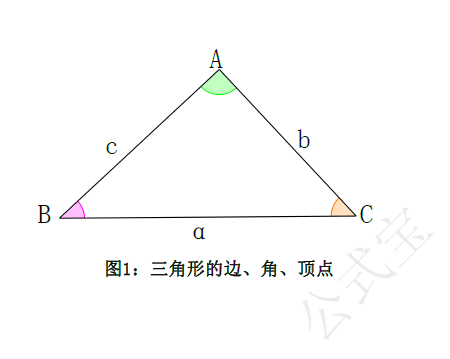
三角形及有关概念

三角形的分类

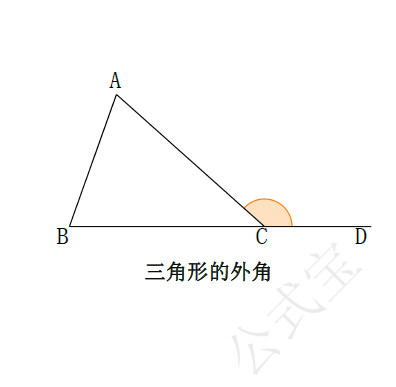
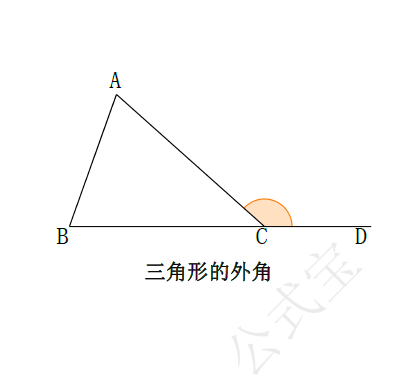
三角形的外角

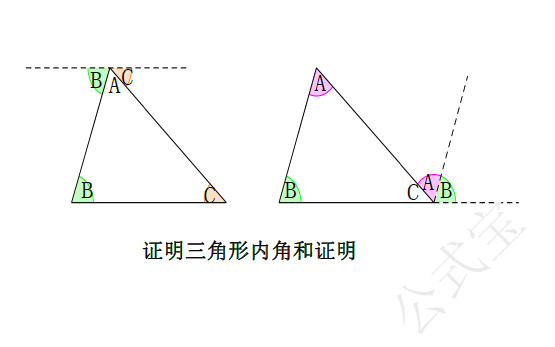
三角形的内角

三角形的外角

直角三角形的性质与判定

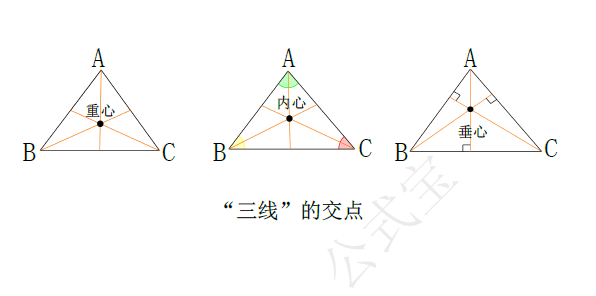
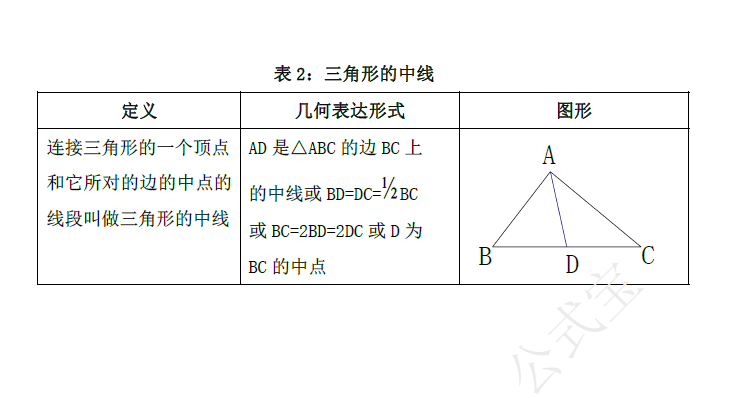
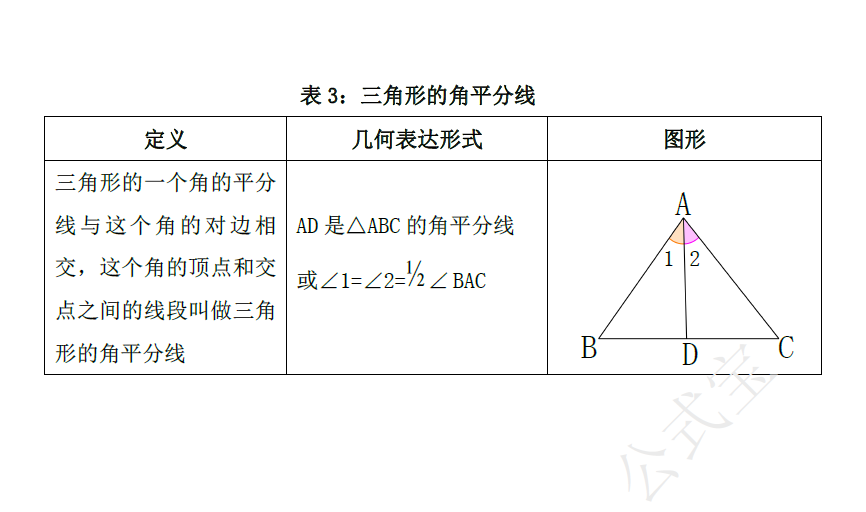
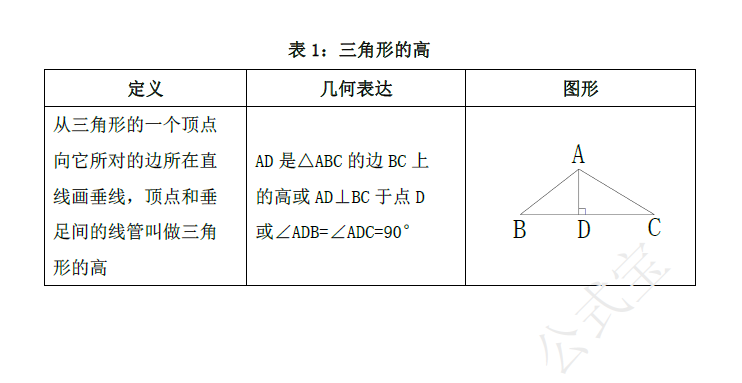
三角形的高、中线与角平分线

“三线”的交点