一般地,在平面直角坐标系中,如果曲线上任意一点的坐标$x,y$都是某个变数$t$的函数
$$\begin{cases}x&=f(t), \\y&=g(t), \end{cases}$$
并且对于$t$的每一个允许值,由方程组所确定的点$M(x,y)$都在这条曲线上,那么方程就叫作这条曲线的参数方程,联系变数$x,y$的变数$t$叫作参变数,简称参数。相对于参数方程而言,直接给出点的坐标间关系的方程叫作普通方程。
参数方程与普通方程的互化
曲线的参数方程和普通方程是曲线方程的不同形式。一般地,可以通过消去参数而从参数方程得到普通方程。如果知道变数$x,y$中的一个与参数$t$的关系,例如$x=f(t)$,把它带入普通方程,求出另一个变数与参数的关系$y=g(t)$,那么$$\begin{cases}x&=f(t), \\y&= g(t),\end{cases}$$就是曲线的参数方程。在参数方程与普通方程的互化中,必须使$x,y$的取值范围保持一致。
把参数方程化为普通方程,需要根据其结构特征,选取适当的消参方法。常见的消参方法有:代入消参法;加减消参法;平方和(差)消参法;乘法消参法等。
把曲线$C$的普通方程$$F(x,y)=0$$化为参数方程的关键:一是适当选取参数;二是确保互化前后方程的等价性。
直线的参数方程
经过点$P_{0}(x_{0},y_{0})$,倾斜角为$\alpha$的直线的参数方程为$$\begin{cases}x=x_{0}+t\cos\alpha, \\y= y_{0}+t\sin\alpha , \end{cases}$$其中$t$为参数。
圆的参数方程
圆$(x-a)^{2}+(y-b)^{2}=r^{2}$的参数方程为$$\begin{cases}x=a+r\cos\theta, \\ y= b+r\sin\theta \end{cases}$$其中$\theta$为参数。特别地,圆心在原点,半径为$r$的圆的参数方程为$$\begin{cases}x=r\cos\theta, \\y= r\sin\theta .\end{cases}$$其中$\theta$为参数。
椭圆
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a > b > 0)$的一个参数方程为$$\begin{cases}x=a\cos\varphi, \\ y= b\sin\varphi . \end{cases}$$其中$\varphi$为参数。通常规定$\varphi$的范围为$\varphi\in[0,2\pi).$
双曲线
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a > b > 0)$的一个参数方程为$$\begin{cases}x=a\sec\varphi, \\ y= b\tan\varphi .\end{cases}$$其中$\varphi$为参数。通常规定$\varphi$的范围为$\varphi\in[0,2\pi ),$且$\varphi \neq \frac{\pi}{2},\varphi \neq \frac{3\pi}{2}.$
抛物线
$y^{2}=2px$的参数方程为$$\begin{cases}x=2pt^{2}, \\ y= 2pt .\end{cases}$$其中$t$为参数。
参数$t$表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数。
渐开线
把一条没有弹性的细绳绕在一个圆盘上,在绳的外端系上一支铅笔,将绳子拉紧,保持绳子与圆相切而逐渐展开,那么铅笔会画出一条曲线。
如图一,设开始是绳子外端位于点$A$,当外端展开导点$M$时,因为绳子对圆心角$\varphi $(单位是弧度)的一段弧$\overset{\frown}{AB}$,展开后成为切线$BM$,所以切线$BM$的长就是$\overset{\frown}{AB}$的长,这是动点满足的几何条件。把笔尖画出的曲线叫做圆的渐开线,相应的定圆叫作渐开线的基圆。
以基圆圆心$O$为原点,直线$OA$为$x$轴,建立平面直角坐标系 如图二,设基圆的半径为$r$,绳子外端$M$的坐标为$(x,y).$取$\varphi$为参数,得圆的渐开线的参数方程:$$\begin{cases} x=r(\cos \varphi + \varphi \sin \varphi) ,\\ y=r(\sin \varphi -\varphi \cos \varphi ). \end{cases}(\varphi 是参数)$$
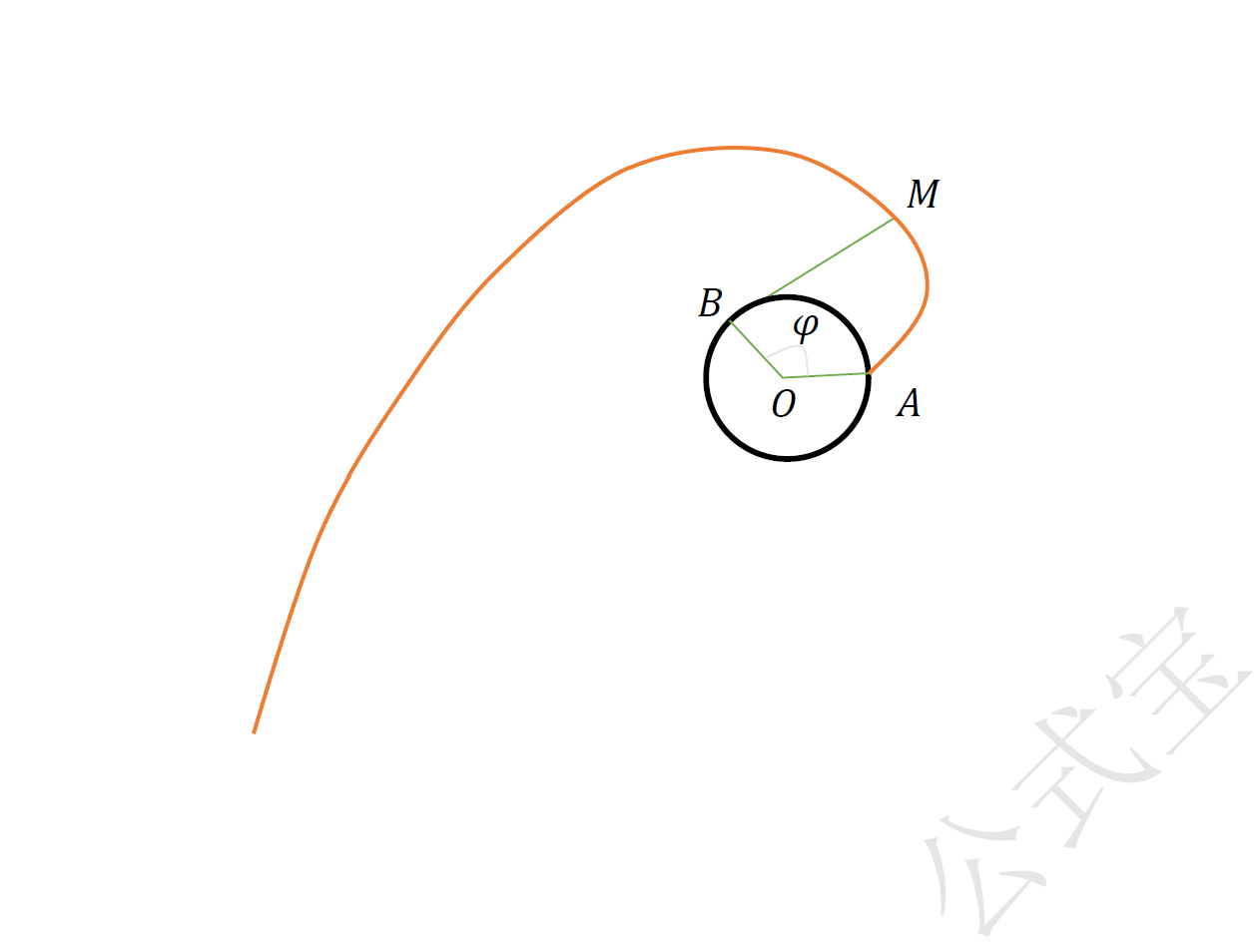
图一
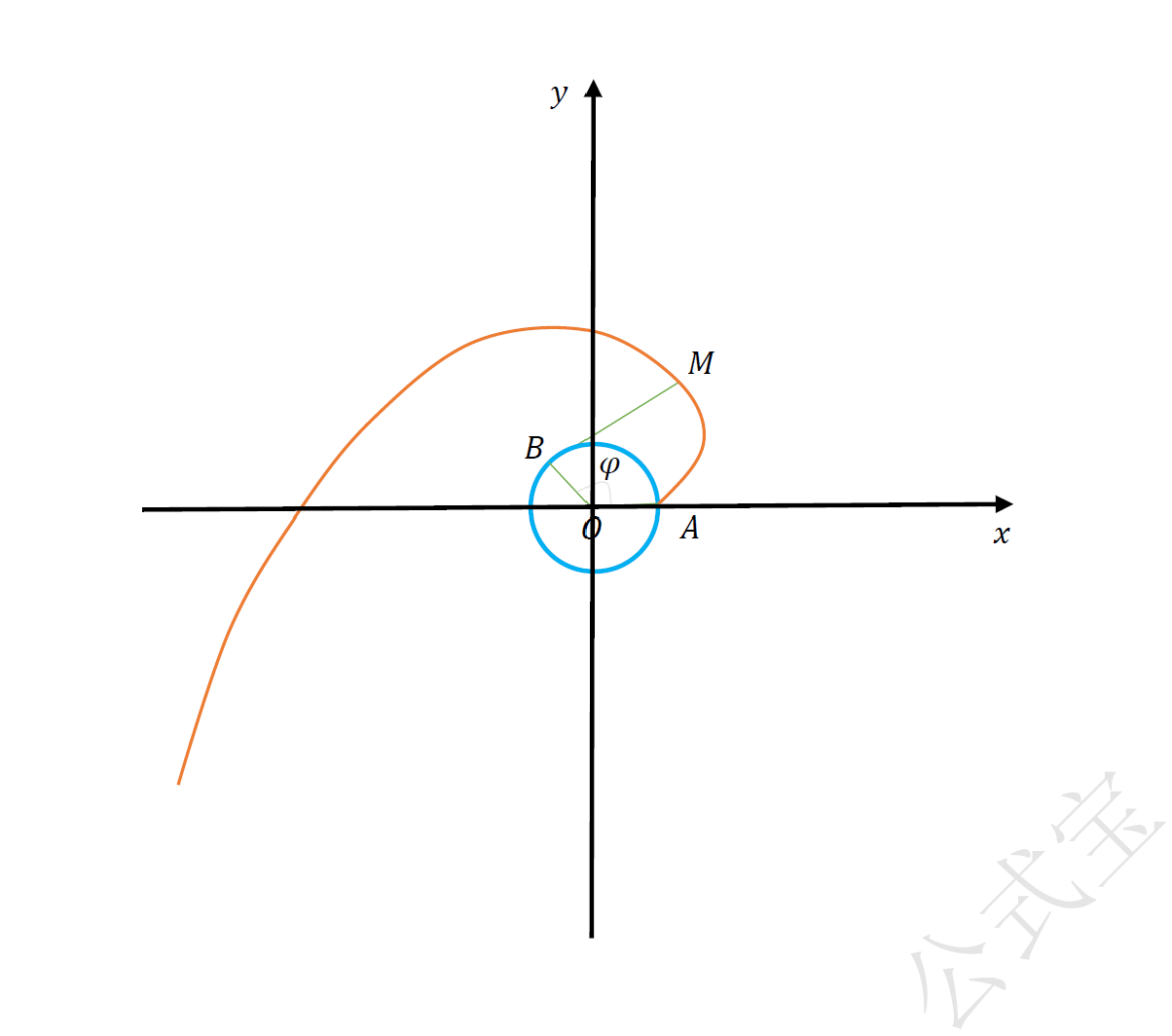
图二
摆线
如图一,一个圆沿着一条定直线无滑动地滚动,假设$B$为圆心,圆周上的定点为$M$,开始时位于$O$处。圆在直线上滚动时,点$M$绕圆心作圆周运动,转过$\varphi$(弧度)角后,圆与直线相切于$A$,线段$OA$的长等于$\overset{\frown}{MA}$的长,即$OA=\varphi$。这就是圆周上的定点$M$在圆$B$沿直线滚动过程中满足的几何条件。把点$M$的轨迹叫作摆线,简称摆线,又叫旋轮线。
取定直线为$x$轴,定点$M$滚动时落在定直线上的一个位置为原点,建立直角坐标系,如图二,设圆的半径为$r$,则摆线的参数方程是$$\begin{cases} x=r(\varphi - \sin \varphi) ,\\ y=r(1 - \cos \varphi ). \end{cases}(\varphi 是参数)$$
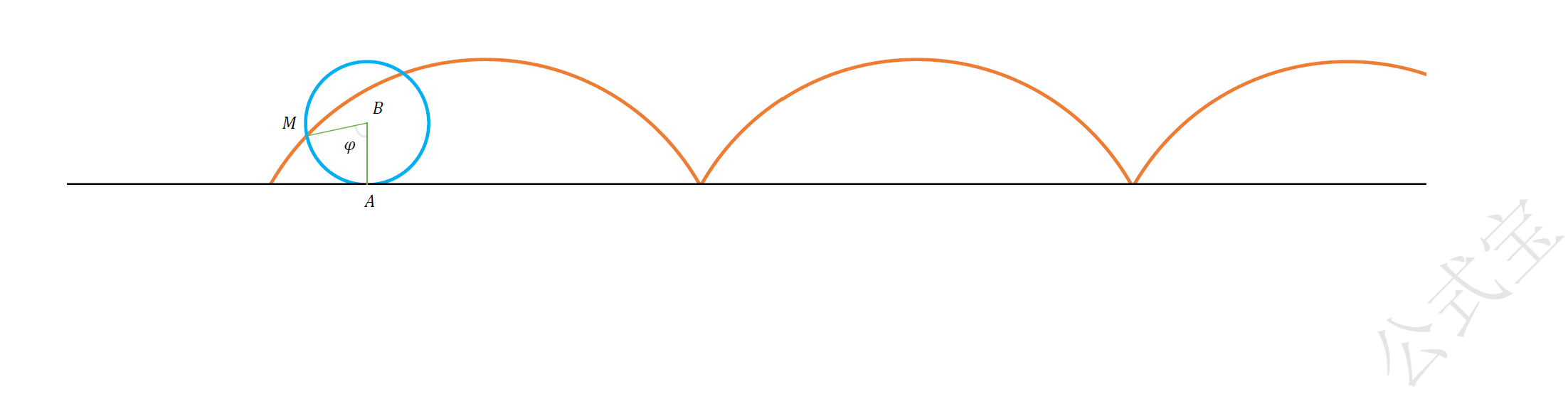
图一
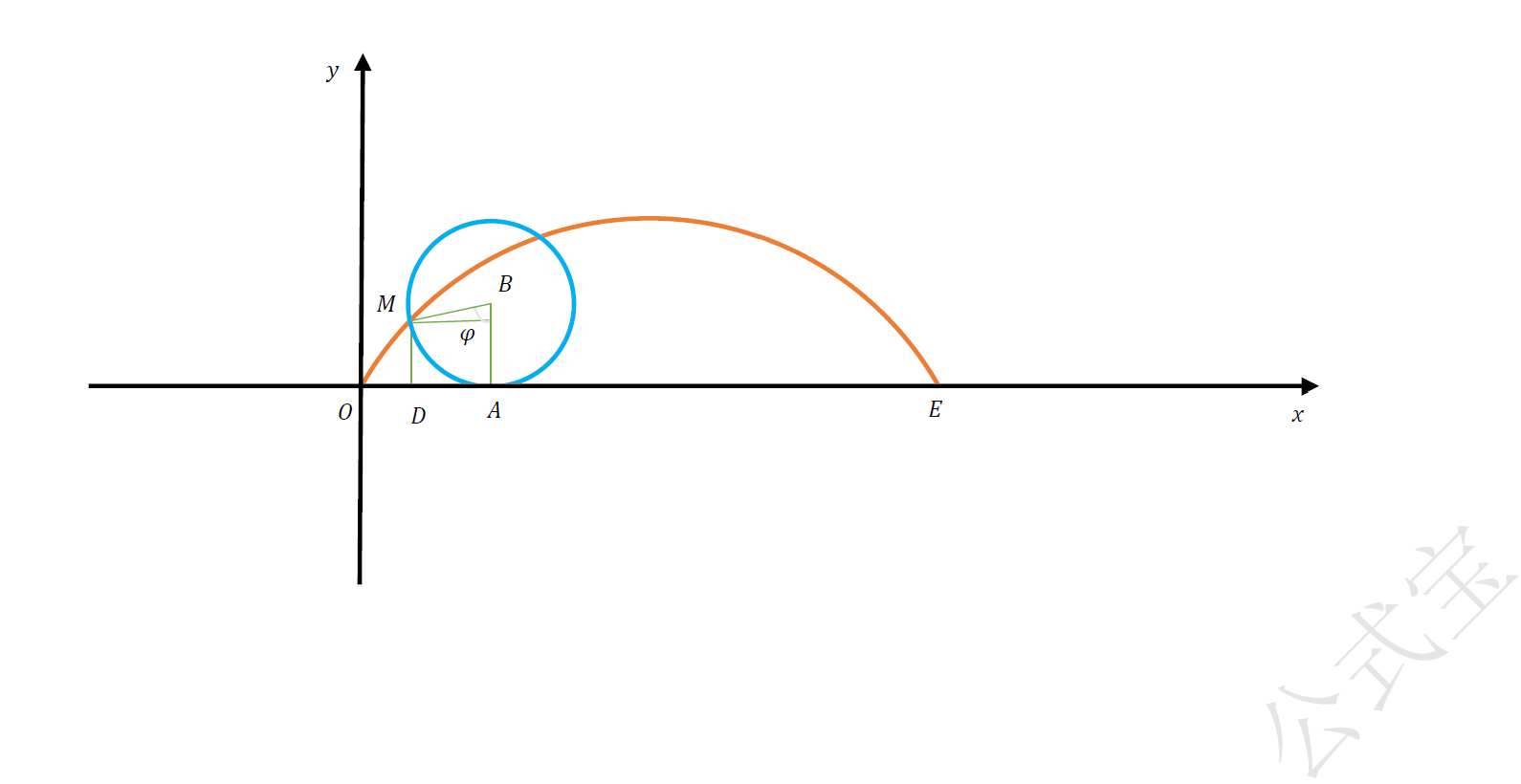
图二