概述
对勾函数是一种类似于反比例函数的一般双曲函数,是形如$f(x)=ax+\frac{b}{x}(ab >0)$的函数。由图像得名,又被称为“双勾函数”“勾函数”“对号函数”“双飞燕函数”等。常见a=b=1。
函数定义
对勾函数是指形如$$f(x)=ax+\frac{b}{x}(ab > 0)$$的函数.
图像
对勾函数的图像是分别以$y$轴和$y=ax$为渐近线的两支曲线,且图像上任意一点到两条渐近线的距离之积恰为渐近线夹角($0-180°$)的正弦值与$|b|$的乘积。
若$a > 0 , b > 0$,在第一象限内,其转折点为$(\sqrt{\frac{b}{a}},2\sqrt{ab})$。
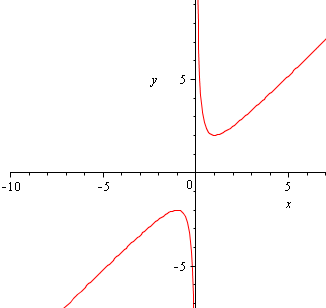
图一 函数图像
最值
当定义域为$(0,+\infty)$时,$f(x)=ax+\frac{b}{x}(a > 0 , b > 0)$在$x=\sqrt{\frac{b}{a}}$处取最小值,最小值为$2\sqrt{ab}$。
当定义域为$(-\infty,0) \cup (0,+\infty)$时,该函数无最值。
当定义域为$(-\infty,0)$时,$f(x)=ax+\frac{b}{x}(a > 0 , b > 0)$在$x=-\sqrt{\frac{b}{a}}$处取最大值,最大值为$-2\sqrt{ab}$。
单调性
令$k=\sqrt{\frac{b}{a}}$,那么:
增区间:$\{x|x ≤ -k\}和\{ x | x ≥ k\}$;
减区间:$\{x| -k ≤ x < 0\}和\{ x | 0 < x ≤ k\}$
变化趋势:在y轴左边先增后减,在y轴右边先减后增。
渐近线
对勾函数的两条渐近线分别为$y$轴、$y=ax$。
1、导数法
$$f(x)=ax+\frac{b}{x}=ax+bx^{-1}$$求导得$f^{\prime}(x)=a-\frac{b}{x^{2}}$
令$f^{\prime}(x)=0,$计算得$x=\pm \sqrt{\frac{b}{a}},$
即对勾函数的转折点横坐标分别为$\sqrt{\frac{b}{a}},-\sqrt{\frac{b}{a}}$。
2、均值不等式法
当$x\in (0,+\infty)$时,由均值不等式$$a+b \geq 2\sqrt{ab}(a > 0 , b > 0)$$将$ax+\frac{b}{x}$中$ax(a > 0)$看做$a$,$\frac{b}{x}$看做b代入上式,得$$ax+\frac{b}{x} \geq 2\sqrt{ax \cdot \frac{b}{x}} = 2\sqrt{ab},$$当且仅当$ax=\frac{b}{x},$即$x=\sqrt{\frac{b}{a}}$时等号成立。故当$x > 0$时,对勾函数的转折点横坐标为$\sqrt{\frac{b}{a}}$。



















