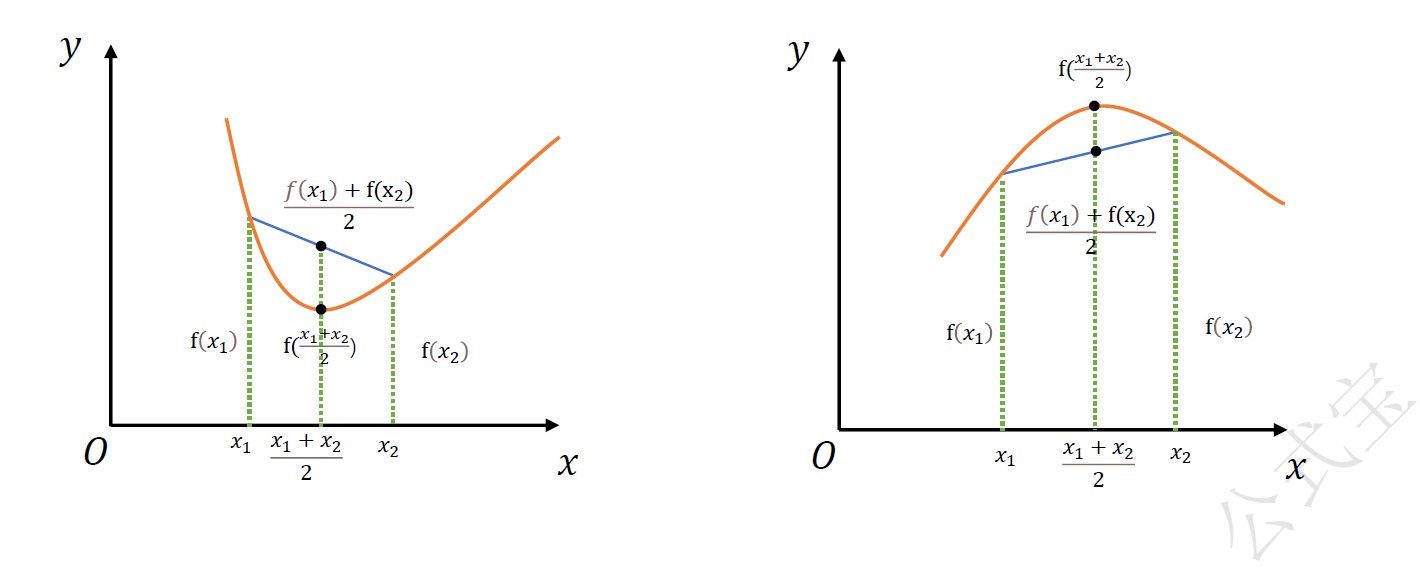凹性
设$f(x)$在区间$I$上连续,如果对$I$上任意两点$x_{1},x_{2}$恒有$$f(\frac{x_{1}+x_{2}}{2}) < \frac{f(x_{1})+f(x_{2})}{2},$$那么称$f(x)$在$I$上的图形是(向上)$\mathbf{凹的}$(或凹弧);
凸性
如果恒有$$f(\frac{x_{1}+x_{2}}{2}) > \frac{f(x_{1})+f(x_{2})}{2},$$那么称$f(x)$在$I$上的图形是(向上)$\mathbf{凸的}$(或凸弧)。
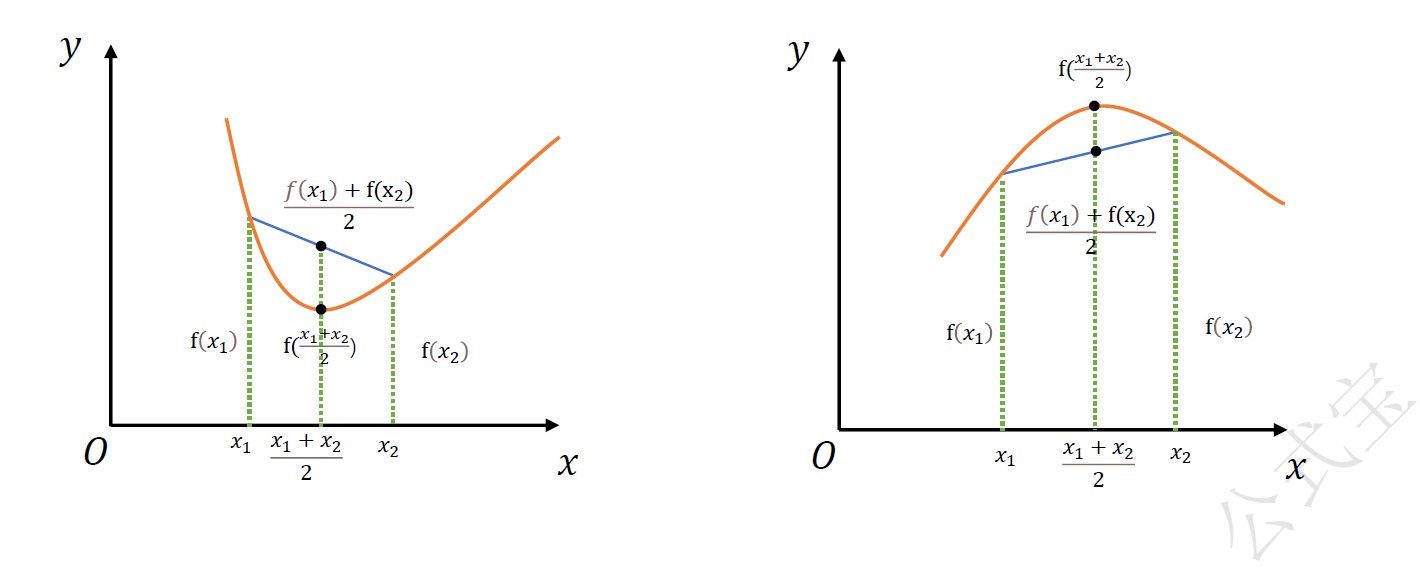
图一 函数的凹凸性
设$f(x)$在$[a,b]$上连续,在$(a,b)$内具有一阶和二阶导数,那么
一、若在$(a,b)$内$$f^{\prime\prime}(x) > 0,$$则$f(x)$在$[a,b]$上的图形是凹的。
二、若在$(a,b)$内$$f^{\prime\prime}(x) < 0,$$则$f(x)$在$[a,b]$上的图形是凸的。
不过补充一下,中国数学界关于函数凹凸性定义和国外很多定义是反的。国内教材中的凹凸,是指的函数图像形状,而不是指函数的性质。在国外,图像的凹凸与直观感受一致,却与函数的凹凸性相反。
另外,国内各不同学科教材、辅导书的关于凹凸的说法也是相反的。一般来说,可按如下方法准确说明:
1、$$f(\frac{x_{1}+x_{2}}{2}) < \frac{f(x_{1})+f(x_{2})}{2},$$ 即V型,为“凸向原点”,或“下凸”(也可说上凹),(有的简称凸有的简称凹)
2、$$f(\frac{x_{1}+x_{2}}{2}) > \frac{f(x_{1})+f(x_{2})}{2},$$即A型,为“凹向原点”,或“上凸”(下凹),(同样有的简称凹有的简称凸)
凸/凹向原点这种说法一目了然。上下凸的说法也没有歧义
在二维环境下,就是通常所说的平面直角坐标系中,可以通过画图直观地看出一条二维曲线是凸还是凹,当然它也对应一个解析表示形式,就是那个不等式。但是,在多维情况下,图形是画不出来的,这就没法从直观上理解“凹”和“凸“的含义了,只能通过表达式,当然n维的表达式比二维的肯定要复杂,但是,不管是从图形上直观理解还是从表达式上理解,都是描述的同一个客观事实。而且,按照函数图形来定义的凹凸和按照函数来定义的凹凸正好相反。
定义
若$f(x)$是区间$[a,b]$上的下凸函数,则对任意的$x_{1},x_{2},x_{3},\dotso ,x_{n} \in [a,b]$,有不等式:$$\frac{\sum\limits_{i=1}^{n}f(x_{i})}{n} \geq f\bigg(\frac{\sum\limits_{i=1}^{n}x_{i}}{n}\bigg)$$当且仅当$x_{1}=x_{2}=x_{3}=\dotso = x_{n}$时等号成立。
加权形式为
若$f(x)$是区间$[a,b]$上的下凸函数,则对任意的$x_{1},x_{2},x_{3},\dotso ,x_{n} \in [a,b]$,且$a_{1}+a_{2}+a_{3}+\dotso + a_{n}=1 ,$ $a_{1},a_{2},a_{3},\dotso a_{n}$为正数,有$$f(a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}+ \dotso +a_{n}x_{n}) \leq a_{1}f(x_{1})+a_{2}f(x_{2})+\dotso + a_{n}f(x_{n})$$当且仅当$x_{1}=x_{2}=x_{3}=\dotso = x_{n}$时等号成立。