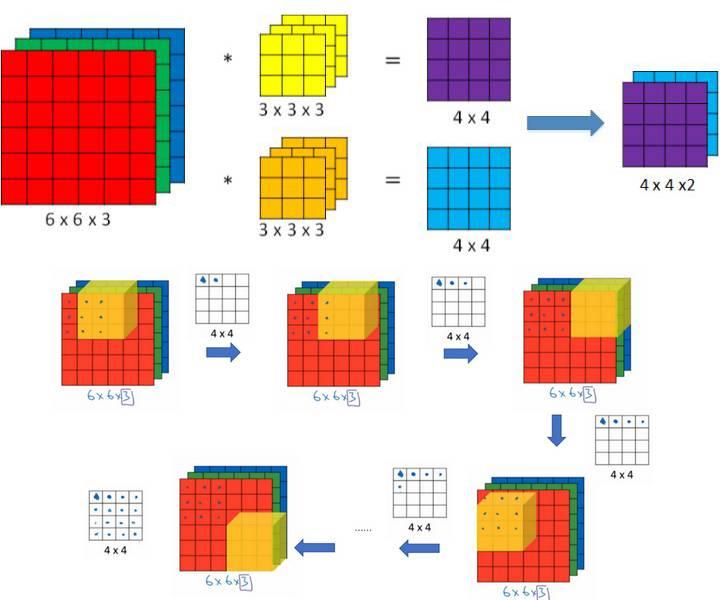
对于行数和列数较多的矩阵$A$，运算时常采用分块法，使大矩阵的运算化成小矩阵运算。将矩阵$A$用若干条纵线和横线分成许多小矩阵，每一个小矩阵称为$A$的子块，以子块为元素的形式上的矩阵称为分块矩阵。

设$A$为$n$阶方阵，若$A$的分块矩阵只有在对角线上有非零子块，其余子块都为零矩阵，且在对角线上的子块都是方阵，即$$A=\begin{bmatrix} A_{1} & & & O \\ & A_{2} & & \\ & & \ddots & \\ O & & & A_{s} \end{bmatrix},$$其中$A_{i}(i=1,2, \dotso , s)$都是方阵，那么称$A$为$\mathbf{分块对角矩阵}$.

分块对角矩阵的行列式具有下述性质$$|A|=|A_{1}||A_{2}| \dotso |A_{s}|.$$由此性质可知，若$|A_{i}| \neq 0(i=1,2, \dotso , s),$则$|A| \neq 0,$并有$$A^{-1}=\begin{bmatrix} A_{1}^{-1} & & & O \\ & A_{2}^{-1} & & \\ & & \ddots & \\ O & & & A_{s}^{-1} \end{bmatrix}.$$

加法

设矩阵$A$与$B$的行数相同、列数相同，采用相同的分块法，有$$\begin{aligned}A&=\begin{bmatrix} A_{11}& \dotso & A_{1r} \\ \vdots & & \vdots \\ A_{s1} & \dotso & A_{sr} \end{bmatrix}, \\ B&=\begin{bmatrix} B_{11}& \dotso & B_{1r} \\ \vdots & & \vdots \\ B_{s1} & \dotso & B_{sr} \end{bmatrix},\end{aligned}$$其中$A_{ij}$与$B_{ij}$的行数相同、列数相同，那么$$A+B=\begin{bmatrix} A_{11}+B_{11}& \dotso & A_{1r}+B_{1r} \\ \vdots & & \vdots \\ A_{s1+}B_{s1} & \dotso & A_{sr}+B_{sr} \end{bmatrix}.$$

数乘

设$A=\begin{bmatrix} A_{11}& \dotso & A_{1r} \\ \vdots & & \vdots \\ A_{s1} & \dotso & A_{sr} \end{bmatrix}$，$\lambda$为数，那么$$\lambda A=\begin{bmatrix} \lambda A_{11}& \dotso & \lambda A_{1r} \\ \vdots & & \vdots \\ \lambda A_{s1} & \dotso & \lambda A_{sr}\end{bmatrix}.$$

矩阵相乘

设$A$为$m \times l$矩阵，$B$为$l \times n$矩阵，分块成$$\begin{aligned}A&=\begin{bmatrix} A_{11}& \dotso & A_{1t} \\ \vdots & & \vdots \\ A_{s1} & \dotso & A_{st} \end{bmatrix}, \\ B&=\begin{bmatrix} B_{11}& \dotso & B_{1r} \\ \vdots & & \vdots \\ B_{t1} & \dotso & B_{tr} \end{bmatrix},\end{aligned}$$其中$A_{i1},A_{i2}, \dotso , A_{it}$的列数分别等于$B_{1j},B_{2j}, \dotso ,B_{tj}$的行数，那么$$AB=\begin{bmatrix} C_{11}& \dotso & C_{1r} \\ \vdots & & \vdots \\ C_{s1} & \dotso & C_{sr} \end{bmatrix},$$其中$$C_{ij}=\sum\limits_{k=1}^{t}A_{ik}B_{kj}(i=1, \dotso ,s;j=1, \dotso ,r).$$

转置

设$A=\begin{bmatrix} A_{11}& \dotso & A_{1r} \\ \vdots & & \vdots \\ A_{s1} & \dotso & A_{sr} \end{bmatrix}$,则$$A^{T}=\begin{bmatrix} A_{11}^{T}& \dotso & A_{s1}^{T} \\ \vdots & & \vdots \\ A_{1r}^{T} & \dotso & A_{sr}^{T} \end{bmatrix}.$$