如果直角三角形的两条直角边长分别为$a,b,$斜边长为$c$,那么$$a^{2}+b^{2}=c^{2}.$$
我国古代称直角三角形的比较短的直角边为勾,较长的直角边为股,斜边为弦。
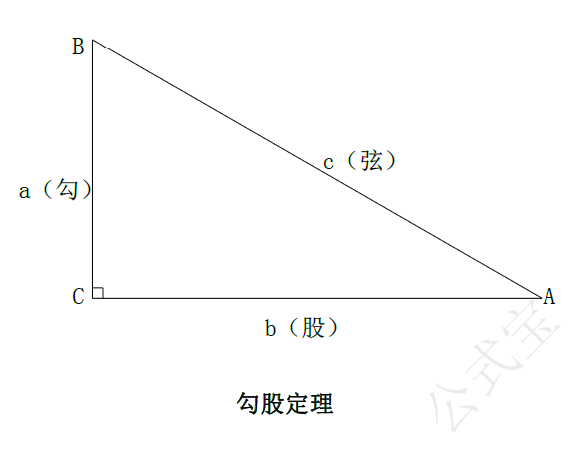
图一 勾股定理
一般是通过剪拼,借助面积进行证明。其中的依据是图形经过补割拼接后,只要没有重叠,没有空隙,面积不变。
图1是由4个全等直角三角形拼成的,得到一个以$a+b$为边长的大正方形和以直角三角斜边$c$为边的小正方形。则大正方形的面积可以表示为$(a+b)^{2}$,又可表示为$\dfrac{1}{2}ab\cdot4+c^{2}$,所以$$(a+b)^{2}=\dfrac{1}{2}ab\cdot4+c^{2},$$整理得$a^{2}+b^{2}=c^{2}$。
在图2的另一种拼法中,以$c$为边长的正方形的面积可表示成四个全等的直角三角形与边长为$(b-a)$的正方形的面积的和。所以$$\dfrac{1}{2}ab\cdot4+(b-a)^{2}=c^{2},$$整理得$a^{2}+b^{2}=c^{2}$。
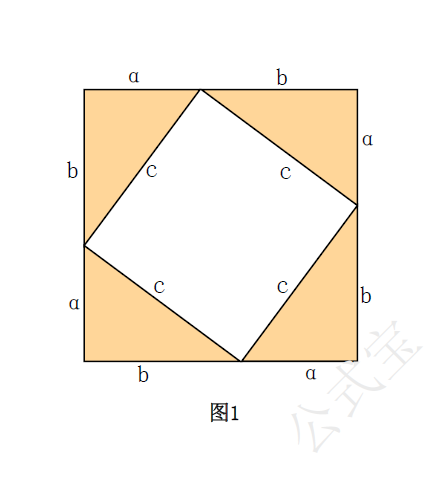
图一 勾股定理
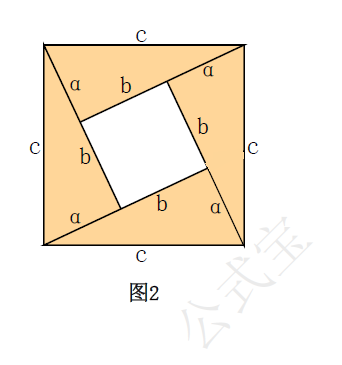
图二 勾股定理的证明
如果三角形的三边长$a,b,c$满足$$a^{2}+b^{2}=c^{2},$$那么这个三角形是直角三角形。
几何语言
如图,$\triangle ABC$中,$$\begin{aligned}&\because a^{2}+b^{2}=c^{2},\\ &\therefore\triangle ABC为直角三角形,且∠C=90^{\circ}.\end{aligned}$$
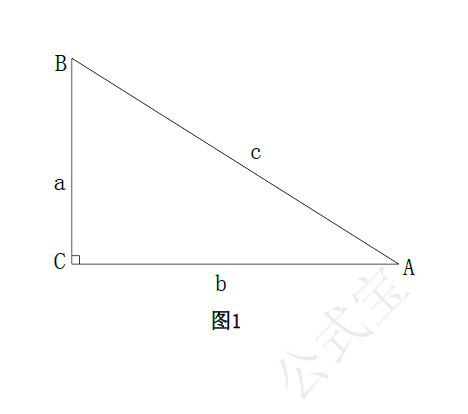
图三 勾股定理的逆定理
联系
两者都与三角形的边有关,且都包含等式$$a^{2}+b^{2}=c^{2};$$
两者都与直角三角形有关;
两者互为逆定理。
区别
勾股定理是以“一个直角三角形”为条件,进而得到直角三角形三边的数量关系,即$$a^{2}+b^{2}=c^{2};$$
勾股定理的逆定理是以“一个三角形的三边满足$$a^{2}+b^{2}=c^{2}$$”的数量关系为条件,进而得到这个三角形是直角三角形,两者的条件和结论相反,前者是直角三角形的性质,而后者是直角三角形的判定。
像8,15,17这样能够成为直角三角形三条边长的三个正整数,称为勾股数。
勾股数组的求法
一、若$a$为大于1的奇数,$b,c$是两个连续自然数,且有$$a^{2}=b+c,$$则$a,b,c$为一组勾股数,例如:
4,5为两个连续自然数,且$3^{2}=4+5$,则3,4,5为一组勾股数,还有5,12,13;7,24,25,;11,60,61$\dots\dots$
二、若$$a,b,c$$为一组勾股数,那么$$ka,kb,kc$$也是一组勾股数,其中$k$为正整数,即勾股数的正整数倍仍是勾股数。例如:3,4,5是一组勾股数,那么6,8,10也是一组勾股数,9,12,15也是一组勾股数。












