含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式。如$$\begin{aligned}x-5>24。\end{aligned}$$
一元一次不等式满足的条件
1.不等号两边都是整式,如$$\frac{2}{x}>3$$不是一元一次不等式,因为不等式左边不是整式形式;
2.不等式中只含有一个未知数,如$$x+y+4>0$$不是一元一次不等式,因为未知数有两个:$x$和$y$;
3.未知数的次数是1。
一元一次不等式是最简单的代数不等式,它是整式形式的不等式,比如$\dfrac{2}{x} >3$不是一元一次不等式。因为未知数$x$在分母中,使得该不等式的左边不是整式形式。
不等式性质
(1)不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变。
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
数字语言简洁表达不等式的性质
性质1:如果$a > b$,那么$a\pm c > b\pm c$
性质2:如果$a > b,c > 0$,那么$ac > bc$(或$a/c > b/c$)
性质3:如果$a > b,c < 0$,那么$ac < bc$(或$\dfrac{a}{c} < \dfrac{b}{c}$)
解一元一次不等式的步骤
去分母(根据不等式的性质2或3):不等式中有分母的要通过不等式两边每一项都乘分母的最小公倍数去分母。注意不要漏乘常数项。
去括号(根据整式运算法则):不等式中有括号的要按照有理数中去括号的法则去括号,在去括号的过程中要注意符号的变化。
移项(根据不等式的性质):就是将不等式右边含未知数的项移到左边来,将左边的常数项变号后移到右边去。
将含未知数项的系数化为1(根据不等式的性质2或3):就是两边都除以$a$将不等式化为$$x\ge\frac{b}{a}$$$$或$$$$x\leq\frac{b}{a}$$的形式。这一过程要根据$a$的符号决定不等号的方向是否改变。
不等式解集
一个有未知数的不等式的所有解,组成这个不等式的解集。例如﹕不等式$x-5\leq -1$的解集为$x\leq 4$;不等式$x> 0$的解集是所有正实数。求不等式解集的过程叫做解不等式。
元一次不等式的解集是一个符合某一个特定条件的一元一次不等式的解的集合,一元一次不等式的解和一元一次不等式的解集是两个不同的概念。它们是从属关系。
将一元一次不等式化为$ax>b$的形式
(1)若$a>0$,则解集为$x>\dfrac{b}{a}$。
(2)若$a<0$,则解集为$x<\dfrac{b}{a}$。
不等式解集表示
(1) 用不等式表示:一般地,一个含未知数的不等式有无数个解,其解集是一个范围,这个范围可用最简单的不等式表达出来,例如:x-1≤2的解集是x≤3。
(2) 用数轴表示:不等式的解集可以在数轴上直观地表示出来,形象地说明不等式有无限多个解,用数轴表示不等式的解集要注意两点:一是定边界线;二是定方向。
(3)能使不等式成立的未知数的值,叫做不等式的解。
求不等式的特殊解
由于不等式的解有无数多个,但若加上一定的条件限制就可以求出它的特殊解,解法如下:
解不等式,求出不等式的解集;
根据题目要求及实际意义利用数轴来确定在一定条件下的特殊解。如:$$\begin{aligned}3x-10\leq0的正整数解为1,2,3。\end{aligned}$$
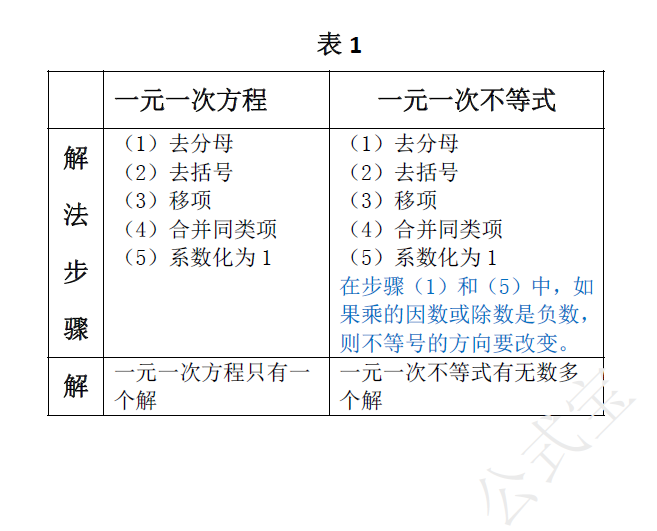
解一元一次不等式与解一元一次方程的方程类似,只是在利用不等式的性质3$$若|a| > |b|,则a^{2} > b^{2}$$对不等式进行变形时。若两边同乘(或除以)负数时要改变不等号的方向,类似表1。
解方程$$ax=b$$与解不等式$$ax> b及ax< b$$的比较,如表2.
一元一次不等式组的概念
一般地,把关于一个未知数的几个一元一次不等式合起来,就组成一个一元一次不等式组。
组成不等式组的每个不等式必须为一元一次不等式。
不等式组中不等式的个数至少是两个。
不等式组中未知数的个数只有一个。
一元一次不等式组的解集
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式的解集,解不等式组就是求它的解集。
一元一次不等式组的解集的数轴表示
求几个一元一次不等式的解集的公共部分通常是利用数轴来确定的。公共部分是指数轴上被各个不等式解集的区域都覆盖的部分。
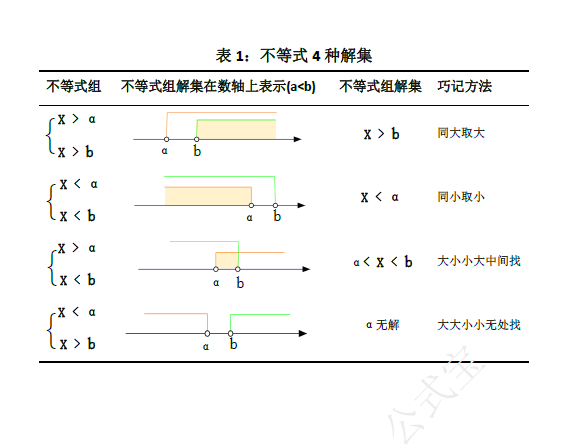
一元一次不等式解集的4种基本类型,如表所示。
一元一次不等式组的解题步骤
求分解,分别解不等式组中的每一个不等式,求出它们的解集;
画公解,将每一个不等式的解集画在同一数轴上,并确定其公共部分;
写组解,将第二步所确定的公共部分表示出来,就是原不等式组的解集。
一元一次不等式组的应用
列一元一次不等式组解应用题的步骤:
$$审题$$$$\Downarrow$$$$设未知数$$$$\Downarrow$$$$找不等关系$$$$\Downarrow$$$$列不等式组$$$$\Downarrow$$$$解不等式组$$$$\Downarrow$$$$检验$$$$\Downarrow$$$$答$$
列不等式组解决实际问题时,求出不等式组的解集后,要结合问题的实际背景,从解集中联系实际找出符合题意的答案。
如求人数或物品的数目、产品的件数等,只能取非负整数。
一元一次不等式组的解集的确定方法
求不等式组的解集,通常采用“分开解”“集中判”的方法。
“分开解”就是分别求出不等式组中各个不等式的解集;
“集中判”就是利用数轴求出各个不等式的解集的公共部分,注意求解口诀的使用。
1、一本英语书98页,孟涛读了7天(一周)还没读完,而张浩不到一周就读完了,张浩平均每天比孟涛多读3页,问孟涛每天读多少页?
解:设孟涛每天读$x$页,则张浩读$(x+3)$页,由题意,得:
$$\dfrac{98}{x} > 7;$$
$$\dfrac{98}{x + 3} < 7$$
解得:$$11< x < 14$$
$∴$孟涛每天读12或13页
$∴x+3=15$或16页
$∴$张浩每天读15或16页
2、把一些书分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本。问这些书有多少本?学生有多少人?
解:设学生有x人 ,由题意,得:
$$3x+8-5(x-1)\geq 0$$
$$3x+8-5(x-1)< 3$$
解得:$$5< x\leq 6.5$$
$∵$由于学生的数量$x$只能取整数,不为小数。
$∴x=6$
$∴$书本有:3×6+8=26(本)
3、用每分钟抽1.1吨水的A型抽水机来抽池水,半小时可以抽完;如果改用B型抽水机,估计20分钟到22分可以抽完。B型抽水机比A型抽水机每分钟约多抽多少吨水?
解:设B型每分钟抽x吨,由题意,得:
$$20x\leq 1.1\times 30$$
$$22x\geq 1.1\times 30$$
解得:$$1.5≤x≤1.65$$
$∴1.5-1.1≤x-1.1≤1.65-1.1$