广义定义
在一个向量空间$V$中,定义在$V \times V$上的正定对称双线性形式函数即是V的数量积,而添加有一个数量积的向量空间即是内积空间。
代数定义
设二维空间内有两个向量$\overrightarrow{a}=(x_{1},Y_{1})$和$\overrightarrow{b}(x_{2},y_{2})$ ,定义它们的数量积(又叫内积、点积)为以下实数:$$\overrightarrow{a}\cdot \overrightarrow{b}=x_{1}x_{2}+y_{1}y_{2}$$
更一般地,n维向量的内积定义如下:$$a\cdot b = \sum\limits_{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\dotso + a_{n}b_{n}.$$
几何定义
两向量$\mathbf{a}$与$\mathbf{b}$的数量积等于$|\mathbf{a}|$、$|\mathbf{b}|$及它们的夹角$\theta$的余弦的乘积,记作$\mathbf{a}\cdot \mathbf{b}$,即$$\mathbf{a}\cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos \theta.$$两向量的数量积等于其中一个向量的模和另一个向量在这向量的方向上的投影的乘积。
$$\mathbf{a}\cdot \mathbf{a}=|\mathbf{a}|^{2}.$$
对于两个非零向量$\mathbf{a}$,$\mathbf{b}$,如果$\mathbf{a}\cdot \mathbf{b}=0$,那么$$\mathbf{a} \bot \mathbf{b}.$$反之,如果$\mathbf{a} \bot \mathbf{b}$,那么$$\mathbf{a} \cdot \mathbf{b}=0.$$
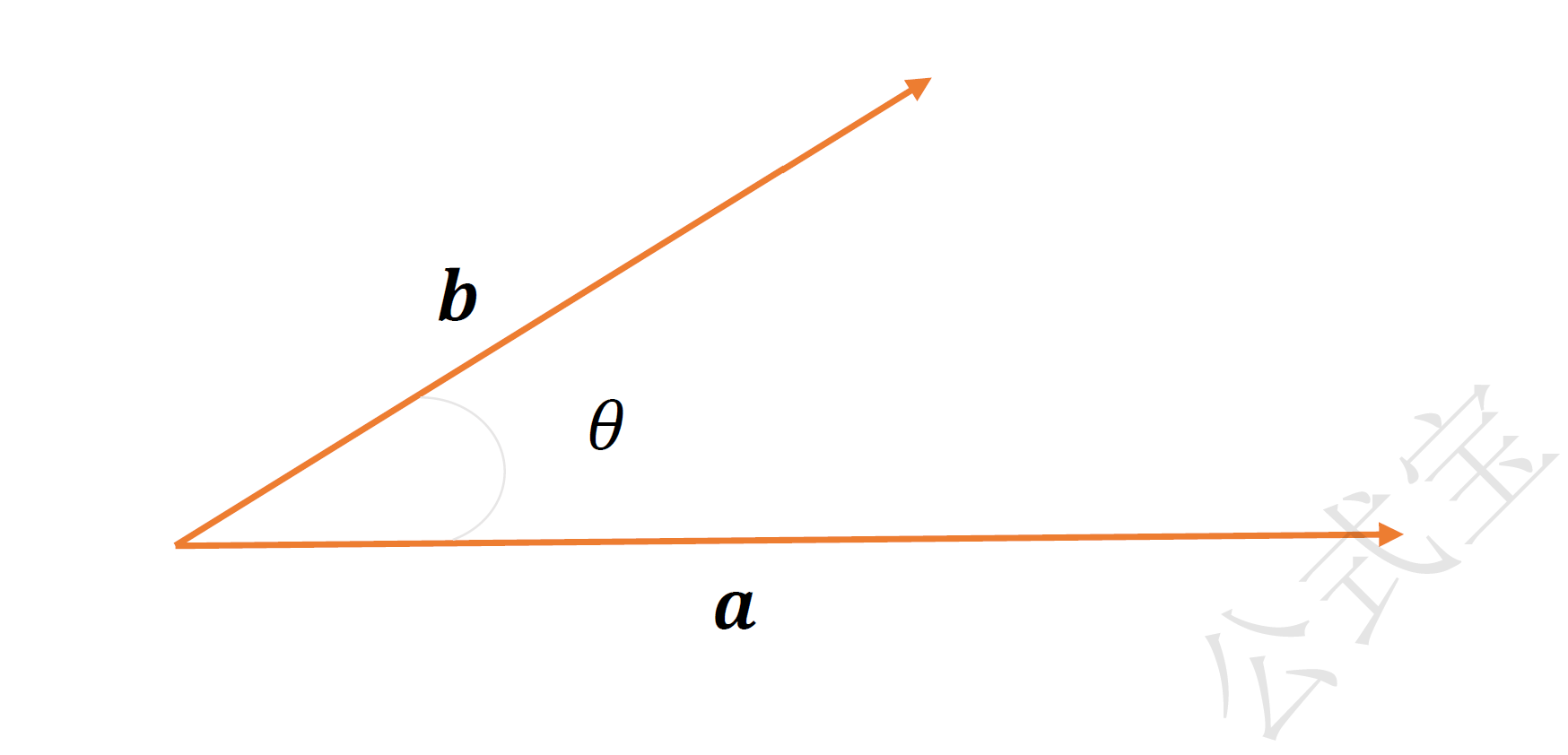
图一 数量积的几何定义
交换律
$$\mathbf{a}\cdot \mathbf{b}=\mathbf{b}\cdot \mathbf{a}.$$
分配律
$$(\mathbf{a}+\mathbf{b})\cdot \mathbf{c}=\mathbf{a}\cdot \mathbf{c}+\mathbf{b}\cdot \mathbf{c}.$$
结合律
$$(\lambda \mathbf{a})\cdot \mathbf{b}=\lambda (\mathbf{a} \cdot \mathbf{b}),\lambda 为数.$$
平面向量的数量积$a \cdot b$是一个非常重要的概念,利用它可以很容易地证明平面几何的许多命题,例如勾股定理、菱形的对角线相互垂直、矩形的对角线相等等。如证明:
勾股定理的证明
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,则$$|CA|^{2}+|CB|^{2}=|AB|^{2}$$
$\because AB=CB-CA$
$\therefore AB^{2}=(CB-CA)^{2}=CB\cdot CB-2CA\cdot CB+CA \cdot CA$
又$\because \angle C = 90^{\circ}$,有$CA \bot CB$,于是$CA \cdot CB = 0$
$\therefore Ab^{2}=AC^{2}+BC^{2}$
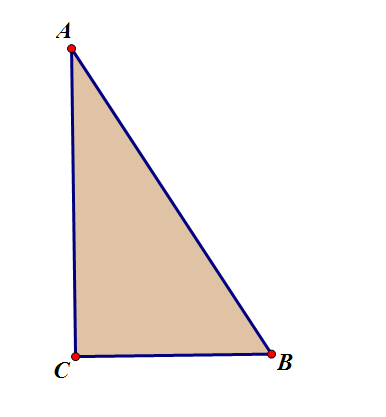
图二 直角三角形
菱形对角线相互垂直
菱形ABCD中,点O为对角线AC、BD的交点,求证AC⊥BD。
设 |AB|=|BC|=|CD|=|DA|=a
∵AC=(AB+BC),BD=(BC+CD)
∴AC·BD=(AB+BC)·(BC+CD)=a²cos(π-α)+a²-a²+a²cosα
又∵ cosα=-cos(π-α)
∴AC·BD=(AB+BC)·(BC+CD)=0
∴AC⊥BD
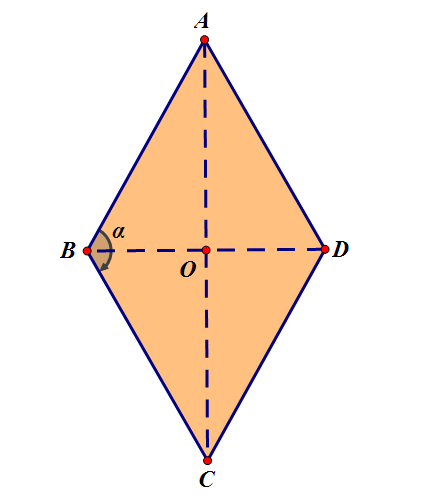
图三 棱形
在生产生活中,点积同样应用广泛。利用点积可判断一个多边形是否面向摄像机还是背向摄像机。向量的点积与它们夹角的余弦成正比,因此在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物理离光照的轴线越近,光照越强。物理中,点积可以用来计算合力和功。若b为单位矢量,则点积即为a在方向b的投影,即给出了力在这个方向上的分解。功即是力和位移的点积。计算机图形学常用来进行方向性判断,如两矢量点积大于0,则它们的方向朝向相近;如果小于0,则方向相反。矢量内积是人工智能领域中的神经网络技术的数学基础之一,此方法还被用于动画渲染(Animation-Rendering)。
线性变换中点积的意义:
根据点积的代数公式:$a\cdot b=a_{1}b_{1}+a_{2}b_{2}+……+a_{n}b_{n}$,假设a为给定权重向量,b为特征向量,则a·b其实为一种线性组合,函数F(a·b)则可以构建一个基于$a\cdot b+c = 0$ (c为偏移)的某一超平面的线性分类器,F是个简单函数,会将超过一定阈值的值对应到第一类,其它的值对应到第二类。





















