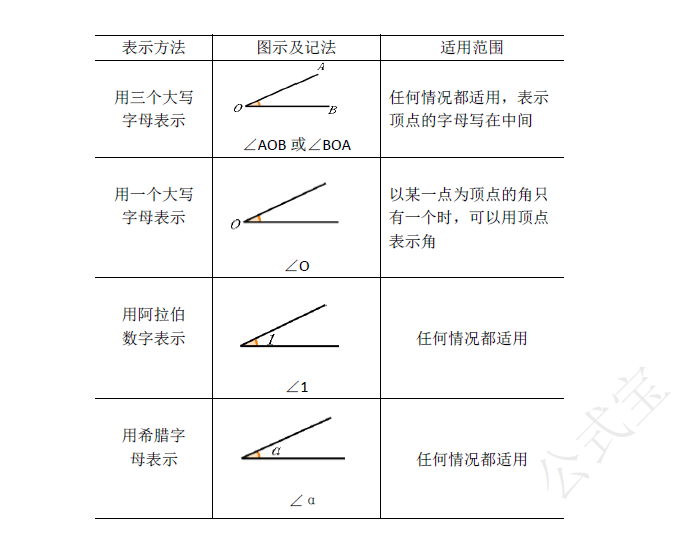
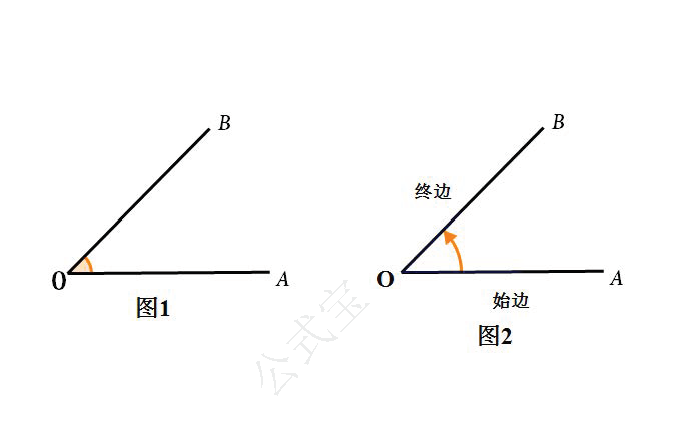
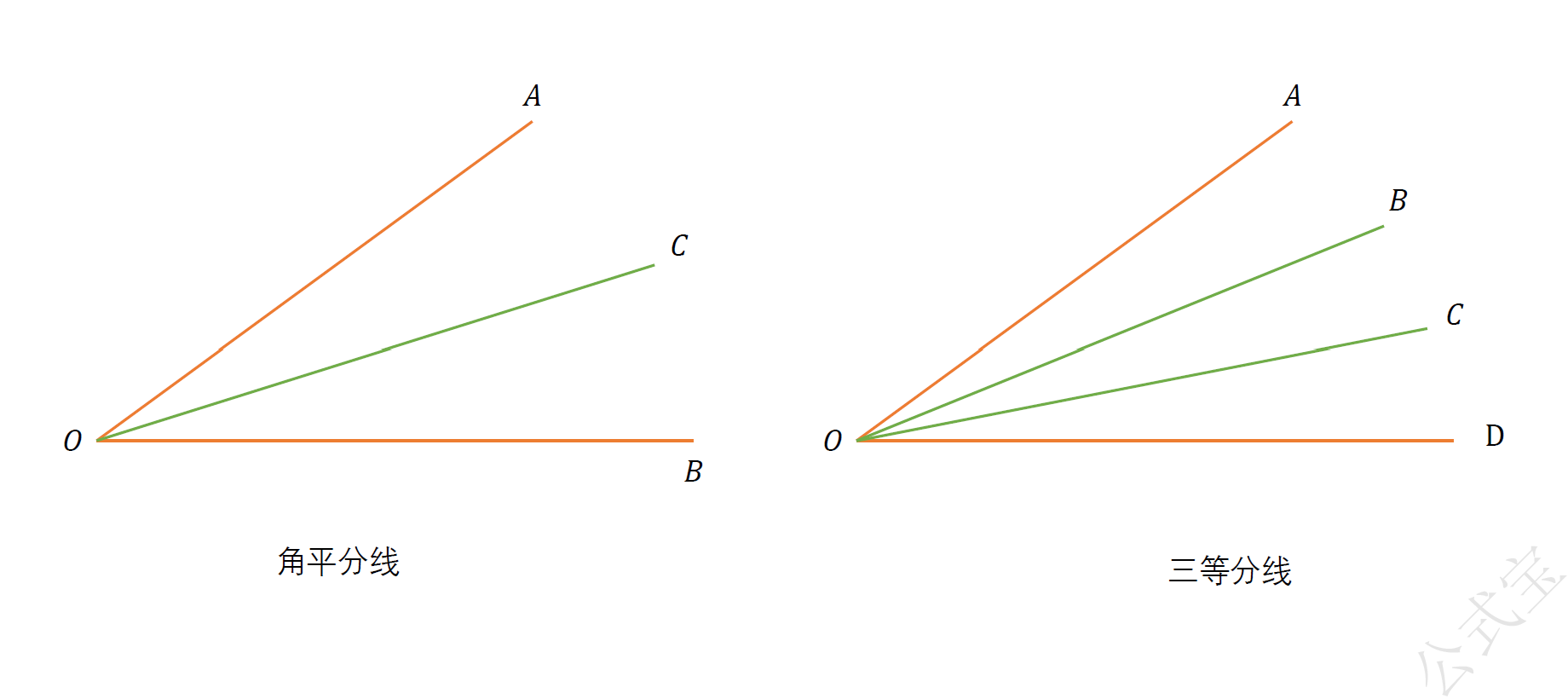一、有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。如图1,$$点O是角的顶点,OA,OB是角的两条边。$$
二、角也可以看作由一条射线绕着它的端点旋转而形成的图形,把起始点位置的射线叫始边,终止位置的射线叫终边。如图2,$$图中的角可以看作射线OA绕着点O旋转到OB而形成的。$$
角的大小与角两边的长短无关,只与构成角的两边的两条射线张开的幅度大小有关。
角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、零角这10种。以度、分、秒为单位的角的度量制称为角度制。此外,还有密位制、弧度制等。
锐角($acute angle$)
大于0$^{\circ}$,小于90$^{\circ}$的角叫做锐角。$^{ [3]}$
直角($right angle$)
等于90$^{\circ}$的角叫做直角。
钝角($obtuse angle$)
大于90$^{\circ}$而小于180$^{\circ}$的角叫做钝角。
1、钝角是由两条射线构成的。
2、钝角是劣角的一种。
3、钝角一定是第二象限角,第二象限角不一定是钝角。
4、钝角的三角函数值中,正弦值($sin$)是正值,余弦值($cos$)、正切值($tan$)、余切值($cot$)是负值。
优角$(major angle)$
大于180$^{\circ}$小于360$^{\circ}$叫优角。
劣角$(minor angle)$
大于0$^{\circ}$小于180$^{\circ}$叫做劣角,锐角、直角、钝角都是劣角。
负角$(negative angle)$
按照顺时针方向旋转而成的角叫做负角。
正角$(positive angle)$
逆时针旋转的角为正角。
零角$(zero angle)$
等于0$^{\circ}$的角。
平角、周角
射线$OA$绕点$O$旋转,当终止位置$OB$和起始位置$OA$成一条直线时,所成的角叫做平角。
当起始射线$OA$又回到起始位置时,所成的角叫做周角。
如图1所示的为平角,如图2所示的为周角。其中$$\begin{aligned}1平角&=180^\circ,\\1周角&=360^\circ,\\1周角&=2平角=4直角。\end{aligned}$$
用三个大写字母表示角时,表示角的顶点的字母应写在中间,表示两边上的点的字母可交换位置。
当以某一点为顶点的角有两个或两个以上时,其中任意一个角都不能用一个大写字母表示。
角的度量单位主要有度、分、秒。
把一个周角360等分,每一份就是1度的角,记作$$1^\circ ;$$把1度的角60等分,每一份叫做1分的角,记作$$1^{\prime};$$把1分的角60等分,每一份叫做1秒的角,记作$$1^{\prime\prime}.$$即:$$1^\circ=60^{\prime},$$$$1^{\prime}=60^{\prime\prime},$$$$1^{\prime}=(\dfrac{1}{60})^{\circ},$$$$1^{\prime\prime}=(\dfrac{1}{60})^{\prime}.$$
以度、分、秒为单位的角的度量制,叫做角度制。
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
角平分线的基本性质
如果$OC$是$∠ AOB$的平分线,则以下各式均成立:$$∠ BOC=∠ AOC; $$$$∠AOB=2∠AOC=2∠BOC; $$$$∠AOC=\dfrac{1}{2}∠AOB,∠BOC=\dfrac{1}{2}∠ AOB.$$
角的三等分线
如果$$∠ AOB=∠ BOC=∠COD=\dfrac{1}{3}∠ AOD,$$那么$OB$,$OC$是$∠AOD$的三等分线。
叠合法
如图,移动$∠DEF$,使它的顶点$E$移到和$∠ABC$的顶点$B$重合,一边$ED$和$BA$重合,另一边$EF$和$BC$落在$BA$的同旁,
如果$EF$和$BC$重合(如图1),那么$DEF$等于$∠ABC$,记作$$∠DEF=∠ABC;$$
如果$EF$落在$∠ABC$的外部(如图2),那么$∠DEF$大于$∠ABC$,记作$$∠DEF>∠ABC;$$
如果$EF$落在$∠ABC$的内部(如图3),那么$∠DEF$小于$∠ABC$,记作$$∠DEF<∠ABC.$$
用这种方法比较两个角的大小,一定要使两个角的顶点及一边重合,另一边落在这条重合边的同旁。
度量法
比较角的大小,可先用量角器分别量出每个角的度数,然后按照度数来比较角的大小。
如$\angle1=30^{\circ}$,$\angle2=60^{\circ}$,$∠1<∠2$。
两角的和与差
角与线段相同,可以用和与差表示角的关系,如下图1,设有两个角$∠1$和$∠2$($∠1>∠2$),把$∠2$移到$∠1$上,使它们的顶点重合,一边重合。
当$∠2$在$∠1$的外部时(如图2),它们的另外两边所成的角$∠ABC$是它们的和,记作$$∠ABC=∠1+∠2;$$
当$∠2$在$∠1$的内部时(如图3),它们的另两边所成的角∠DEF是它们的差,记作$$∠DEF=∠1-∠2.$$
角的倍与分
如果2个$∠1$的和是$∠2$,那么$∠2$是$∠1$的2倍,记作$$∠2=2∠1;$$$∠1$是$∠2$的$\dfrac{1}{2}$,记作$$∠1=\dfrac{1}{2}∠2.$$
如果3个$∠1$的和是$∠3$,那么$∠3$是$∠1$的3倍,记作$$∠3=3∠1;$$$∠1$是$∠3$的$\dfrac{1}{3}$,记作$$∠1=\dfrac{1}{3}∠3.$$
余角及其性质
如果两个角的和等于$90^\circ$(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角。用数学语言表示:若$$∠ \alpha+∠ \beta=90^{\circ}$$则$∠ \alpha与∠ \beta$互余;反之,若$$∠ \alpha与∠ \beta互余,$$则$∠ \alpha+∠ \beta=90^{\circ}.$
余角的性质:同角(等角)的余角相等。
补角及其性质
如果两个角的和等于$180^\circ$(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角。用数学语言表示:若$$∠ \alpha+∠ \beta=180^{\circ},$$则$∠ \alpha与∠ \beta互补$;反之,若$$∠ \alpha与∠ \beta互补,$$则$∠ \alpha+∠ \beta=180^{\circ}.$
补角的性质:同角(等角)的补角相等。
互为余角、补角是两个角之间的关系,如$$∠ 1+∠ 2+∠ 3=180^{\circ},$$不能说$∠1,∠2,∠3$互为补角。
余角和补角
两角之和为90$^{\circ}$则两角互为余角,两角之和为180$^{\circ}$则两角互为补角。等角的余角相等,等角的补角相等。
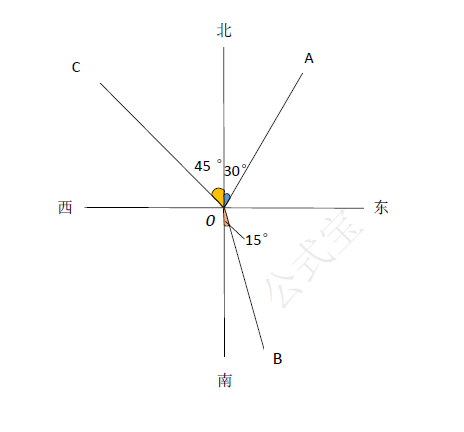
方向角
在航行和测绘等工作中,经常要用到表示方向的角。例如图中:$$\begin{aligned}&射线OA的方向是北偏东30^{\circ};\\&射线OB的方向是南偏东15^{\circ},\end{aligned}$$这里的“北偏东$30^{\circ}$”和南偏东$15^{\circ}$是用来表示方向的角,叫做方向角。
图中有正东、正西、正南、正北4个方向不需要用角度来表示。
方向角必须以正北或正南方向作为基准。“北偏东$30^{\circ}$”不能说成“东偏北$60^{\circ}$”,“南偏西$30^{\circ}$”不能说成“西偏南$60^{\circ}$”。
对顶角
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。两条直线相交,构成两对对顶角。互为对顶角的两个角相等。
邻补角
两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角。
内错角
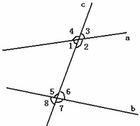
两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫做内错角(alternate interior angle )。如:$∠1$和$∠6$,$∠2$和$∠5$。
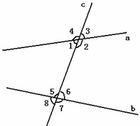
图一 内错角
同旁内角
两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角,如:$∠1$和$∠5$,$∠2$和$∠6$。
同位角
两个角都在截线的同旁,又分别处在被截的两条直线同侧,具有这样位置关系的一对角叫做同位角$(corresponding angles)$:$∠1$和$∠8$、$∠2$和$∠7$。
外错角
两条直线被第三条直线所截,构成了八个角。如果两个角都在两条被截线的外侧,并且在截线的两侧,那么这样的一对角叫做外错角。例如:$∠4$与$∠7$,$∠3$与$∠8$。
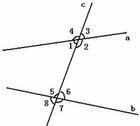
图一 外错角
同旁外角
两个角都在截线的同一侧,且在两条被截线之外,具有这样位置关系的一对角互为同旁外角。如:$∠4$和$∠8$,$∠3$和$∠7$。
终边相同的角
具有共同始边和终边的角叫终边相同的角。与角$a$终边相同的角属于集合:
$A={b|b=k360^{\circ}+a,k\isin Z}$表示角度制内所有角的集合;
$B={b|b=2k\pi+a,k\in Z}$表示弧度制内所有角的集合。
二者实质上是相同的,只是符号表述不同。即,这里$A=B$。
4
直线外一点与直线上各点连接的所有线段中,垂线段最短
11
三角形内角和定理三角形三个内角的和等于180$^{\circ}$
13
推论2 三角形的一个外角等于和它不相邻的两个内角的和
14
推论3 三角形的一个外角大于任何一个和它不相邻的内角
16
边角边公理($SAS$) 有两边和它们的夹角对应相等的两个三角形全等
17
角边角公理($ASA$)有两角和它们的夹边对应相等的两个三角形全等
18
推论($AAS$) 有两角和其中一角的对边对应相等的两个三角形全等
19
斜边、直角边公理($HL$) 有斜边和一条直角边对应相等的两个直角三角形全等
20
定理1 在角的平分线上的点到这个角的两边的距离相等
21
定理2 到一个角的两边的距离相同的点,在这个角的平分线上
22
角的平分线是到角的两边距离相等的所有点的集合
23
等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角)
25
推论2 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
26
推论3 等边三角形的各角都相等,并且每一个角都等于60$^{\circ}$
27
等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
29
推论2 有一个角等于60$^{\circ}$的等腰三角形是等边三角形
30
在直角三角形中,如果一个锐角等于$30^{\circ}$那么它所对的直角边等于斜边的一半
32
定理 线段垂直平分线上的点和这条线段两个端点的距离相等
33
逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
34
线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
35
定理 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线














.png)