邻补角
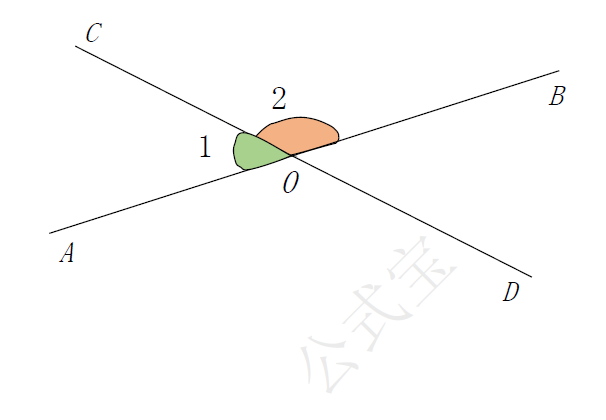
如图,$∠ 1$和$∠ 2$有一条公共边$OC$,它们的另一边互为反向延长线($∠ 1$和$∠ 2$互补),具有这种关系的两个角,互为邻补角。
邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角。
邻补角是成对出现的。
对顶角
如图,$∠ 1$和$∠ 3$有一个公共顶点$O$,并且$∠ 1$的两边分别是$∠ 3$的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
对顶角(与位置有关)一定相等,但相等的角(与位置无关)不一定是对顶角。
对顶角表示的是两个角的位置关系,总是成对出现的,不能说某一个角是对顶角。
对顶角、邻补角的识别方法
判断对顶角和邻补角,首先是看两个角两边涉及的直线是否只有两边,还应注意对顶角没有公共边,邻补角有公共边,两条直线相交形成的四个角中,共有两对对角,四对邻补角。
垂直的定义
在相交线的模型中,固定木条$a$,转动木条$b$。当$b$的位置变化时,$a,b$所成的$∠\alpha$也会发生变化。当$∠\alpha=90^{\circ}$时,我们说$a$与$b$互相垂直,记作$$a\perp b.$$
垂线的定义
垂直是相交的一种特殊情形,两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。如果$AB\perp CD$,交点为$O$,那么垂足为$O$。
根据定义可知,当两条直线垂直时,相交所成的4个角均为直角;反之,若两条直线相交所成的4个角中任意一个为直角,则两条直线互相垂直。
垂线的性质
在同一平面内,过一点且只有一条直线与已知直线垂直。
连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短。
点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
区分两点间的距离与点到直线 距离:
两点间的距离:连接两点的线段的长度。其性质是:$$是两点之间,线段最短。$$
点到直线的距离:直线外一点到这条直线的垂线段的长度。其性质是:$$垂线最短。$$
垂线是直线,垂线段是一条线段,点到直线的距离是指垂线段的长度,是一个数量,是有单位的。
在图形中确定点到直线的距离,首先要作出这点到直线的垂线段,然后求垂线段的长度。
两条直线被第三条直线所截形成八个角,它们构成同位角、内错角及同旁内角。
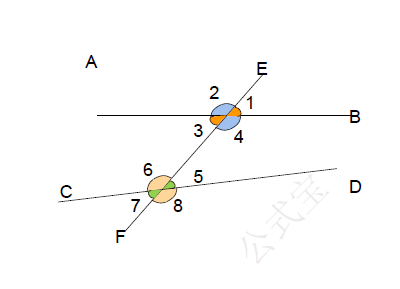
如图,直线$AB,CD$与$EF$相交(也可以说两条直线$AB,CD$被第三条直线$EF$所截),构成八个角。
同位角
图中$∠1$与$∠5$,这两个角分别在直线$AB,CD$的同一方(上方),并且都在直线$EF$的同侧(右侧),具有这种位置关系的一对角叫做同位角。$∠2$和$∠6$,$∠4$和$∠8$,$∠3$和$∠7$都是同位角。
内错角
图中$∠3$与$∠5$,这两个角都在直线$AB,CD$之间,并且分别在直线$EF$两侧($∠3$在直线$EF$左侧,$∠5$在直线$EF$右侧),具有这种位置关系的一对角叫做内错角,$∠4$和$∠6$也是内错角。
同旁内角
:图中$∠3$与$∠6$也都在直线$AB < CD$之间,但它们在直线$EF$的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角。$∠4$和$∠5$也是同旁内角。













.png)