全内反射，又称全反射（total internal reflection，TIR），是一种光学现象。当光线从较高折射率的介质进入到较低折射率的介质时，如果入射角大于某一临界角θc（光线远离法线）时，折射光线将会消失，所有的入射光线将被反射而不进入低折射率的介质。

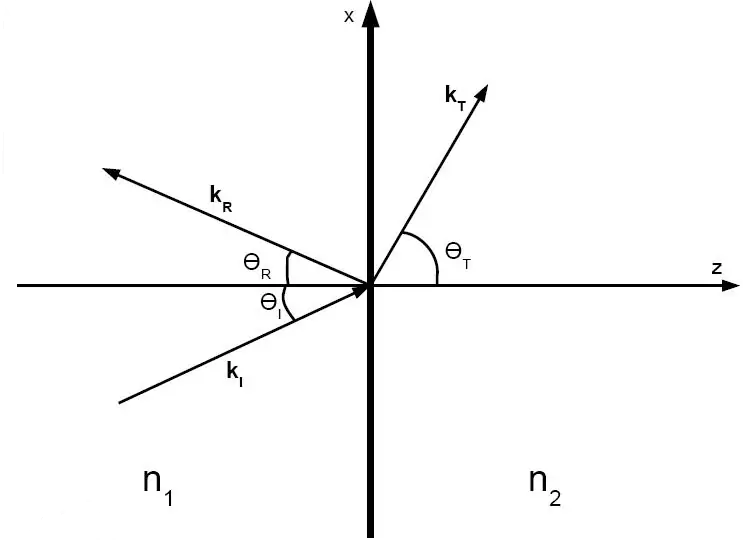
如图一所示，光线从折射率较高的$n_1$介质进入折射率较低的$n_2$介质。

当入射角$θ_{1}$时，光线同时发生向$n_{2}$介质中的折射，以及向$n_{1}$介质中的反射（图一中红色光线所示）；

当入射角$θ_{2}$ > 临界角$θ_{c}$时，向n2介质中折射的光线消失，所有光线向n1介质中反射（图一中蓝色光线所示）；

全内反射仅仅可能发生在当光线从较高折射率的介质（也称为光密介质）进入到较低折射率的介质（也称为光疏介质）的情况下，例如当光线从玻璃进入空气时会发生，但当光线从空气进入玻璃则不会。

临界角是折射角为 $90^{\circ}$ 的入射角。相对于在折射边界处来测量入射角（参见斯奈尔定律图）。考虑从玻璃进入空气的光线， 从界面发出的光偏向玻璃板。当入射角度充分增加时，折射角（空气中）达到 $90^{\circ}$ 。入射角是由折射界面的法线量度。临界角 $\theta_{C}$ 可利用折射定律$$n_{1} \sin \theta_{i}=n_{2} \sin \theta_{t}$$ 进行求解。 为了找到临界角，当 $\theta_{t}=90^{\circ}$ 时，我们得到 $\theta_{i}$ ，因此 $\sin \theta_{t}=1 。 \theta_{i}$ 的结果值等于临界角 $\theta_{c}$ 。 现在，我们可以求解 $\theta_{i}$ ，得到临界角方程:$$\theta_{c}=\theta_{i}=\arcsin \left(\frac{n_{2}}{n_{1}}\right)$$ 其中， $n_{2}$ 是较低密度介质的折射率，及 $n_{1}$ 是较高密度介质的折射率。这个公式是斯涅尔定律的一个简单应用。当入射光线是 准确的等于临界角，折射光线会循折射界面的切线进行。以可见光由玻璃进入空气（或真空）为例，临界角约为 $41.5^{\circ}$

在正常条件下，衰逝波在界面上传输零能量。 然而，如果具有较高折射率的第三介质放置在距离第一介质和第二介质之间的界面的距离不到几个波长内，则衰逝波将不同于普通波， 它会将能量传递到第二种介质中。这个过程称为受抑全内反射（FTIR），与量子隧道非常相似。 如果将电磁场认为是光子的波函数，量子隧道模型在数学上是类似的。低折射率介质可以被认为是光子可以穿透的势垒。

FTIR的透射系数对第三介质和第二介质之间的间距高度敏感（直到间隙几乎闭合为止，函数近似为指数），所以这种效应经常用于调制具有大动态的光学透射和反射范围。

一个不太为人所知的全内反射的方面是反射光在反射和入射光之间有一个角度相变，即相移。 在数学上，这意味着菲涅尔反射系数是复数，而不是实数。这种相移是偏振相关的，并且随着入射角与临界角进一步偏离到掠入射角度而增长。