斐波那契数列 (Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契 (Leonardo Fibonacci) 以兔子繁 殖为例子而引入,故又称为 “兔子数列”,指的是这样一个数列: 1、1、2、3、5、8、13、21、34、.....在数学上,斐波那契数列 以如下被以递推的方法定义: $$F(0)=1, F(1)=1, F(n)=F(n-1)+F(n-2)\left(n \geq 2, n \in N^*\right)$$ 在现代物理、准晶体结构、化学等领 域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以 《斐波那契数列季刊》为名的一份数学杂志,用于 专门刊载这方面的研究成果。
定义
斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89...
这个数列从第3项开始,每一项都等于前两项之和。
广义斐波那契数列
斐波那契数列的黄金特征 1 ,还让我们联想到佩尔数列: $1 , 2 , 5 , 12 , 29 , \ldots$, 也有 $\left|2^* 2-1 * 5\right|=|5 * 5-2 * 12|=\ldots=1$ (该类数列 的这种特征值称为勾股特征)。
佩尔数列 $P_n$ 的递推规则: $P_1=1, \quad P_2=2, \quad P_n=P_{n-2}+2 P_{n-1}$.
据此类推到所有根据前两项导出第三项的通用规则: $a_n=p \cdot a_{n-1}+q \cdot a_{n-2}$ ,称为广义斐波那契数列。
当 $p=1, \quad q=1$ 时,我们得到斐波那契一卢卡斯数列。
当 $p=1, \quad q=2$ 时,我们得到佩尔一勾股弦数(跟边长为整数的直角三角形有关的数列集合)。
当 $p=2, \quad q=-1$ 时,我们得到等差数列。其中 $a_1=1, \quad a_2=2$ 时,我们得到自然数列 $1 , 2 , 3 , 4 , 5 \ldots$ 自然数列的 特征就是每个数的平方与前后两数之积的差为 1 (等差数列的这种差值称为自然特征)。
具有类似黄金特征、勾股特征、自然特征的广义―斐波那契数列 $p= \pm 1$ 。
当 $a_1=1, \quad a_2=2, \quad p=2, \quad q=0$ ,时,我们得到等比数列 $1 , 2 , 4 , 8 , 16 \ldots$
递推公式
斐波那契数列: $1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 \ldots$
斐波纳契数列以如下被以递归的方法定义:
$$F(0)=1, F(1)=1, F(n)=F(n-1)+F(n-2)\left(n \geq 2, n \in \mathrm{N}^*\right)$$ 这个数列从第三项开始,每一项都等于前两 项之和。
显然这是一个线性递推数列。
通项公式内容
(1) $$a_n=1 \div \sqrt{5}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$$
(如上,又称为“比内公式”,是用无理数表示有理数的一个范例。 )
注: 此时 $a_1=1, \quad a_2=1, \quad a_n=a_{n-1}+a_{n-2},\left(n \geq 2, \quad n \in \mathrm{N}^*\right)$
(2)$$a_n=\frac{\frac{2}{\sqrt{5}+1}-\frac{1}{\left(\sqrt{5}+\frac{1}{2}\right)^n}}{\sqrt{5}}$$
通项公式推导
方法一: 利用特征方程 (线性代数解法)
线性递推数列的特征方程为:
$$x^2=x+1$$
解得 $x_1=\frac{1+\sqrt{5}}{2}, \quad x_2=\frac{1-\sqrt{5}}{2}$.
则 $a_n=C_1 x_1^n+C_2 x_2^n$
$$\begin{aligned}& \because a_1=a_2=1 \\& \therefore C_1 x_1+C_2 x_2=C_1 x_1^2+C_2 x_2^2=1\end{aligned}$$
解得 $\therefore C_1=\frac{1}{\sqrt{5}}, \quad C_2=-\frac{1}{\sqrt{5}}$.
$$\therefore a_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right] \text {. }$$
方法二: 待定系数法构造等比数列1 (初等代数解法)
设常数 $r, s$ ,
使得 $a_n-r \cdot a_{n-1}=s\left(a_{n-1}-r \cdot a_{n-2}\right)$
则 $r+s=1,-r \cdot s=1$.
$n \geq 3$ 时,有:
$$\begin{aligned}a_n-r \cdot a_{n-1} & =s \cdot\left(a_{n-1}-r \cdot a_{n-2}\right) \\a_{n-1}-r \cdot a_{n-2} & =s \cdot\left(a_{n-2}-r \cdot a_{n-3}\right) \\& \cdots \\a_3-r \cdot a_2 & =s \cdot\left(a_2-r \cdot a_1\right)\end{aligned}$$
联立以上 $n-2$ 个式子,得:
$$\begin{aligned}& a_n-r \cdot a_{n-1}=s^{n-2} \cdot\left(a_2-r \cdot a_1\right) \\& s=1-r, \quad a_1=a_2=1 .\end{aligned}$$
上式可化简得:
$$a_n=s^{n-1}+r \cdot a_{n-1}$$
那么:
$$\begin{aligned}a_n & =s^{n-1}+r \cdot a_{n-1} \\& =s^{n-1}+r \cdot s^{n-2}+r^2 \cdot s^{n-3}+r^3 \cdot a_{n-3} \\& =\cdots \\& \left.=s^{n-1}+r \cdot s^{n-2}+r^2 \cdot s^{n-3}+\ldots \ldots+r^{n-2} \cdot s+r^{n-1} \cdot a_1\right) \\& =s^{n-1}+r \cdot s^{n-2}+r^2 \cdot s^{n-3}+\ldots \ldots+r^{n-2} \cdot s+r^{n-1} \\& =\frac{\left[s^{n-1}-r^{n-1} \cdot r / s\right]}{1-r / s} \\& =\frac{s^n-r^n}{s-r}\end{aligned}$$
(这是一个以 $s^{n-1}$ 为首项、以 $r^{n-1}$ 为末项、 $\frac{r}{s}$ 为公比的等比数列的各项的和)。
$r+s=1, \quad-r \cdot s=1$ , 的解为 $s=\frac{1+\sqrt{5}}{2}, \quad r=\frac{1-\sqrt{5}}{2}$ ,
则 $$a_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right].$$
方法三: 待定系数法构造等比数列 (初等代数解法)
设 $a_n-\alpha \cdot a_{n-1}=\beta\left(a_{n-1}-\alpha \cdot a_{n-2}\right)$,
得 $\left\{\begin{array}{l}\alpha+\beta=1 \\ \alpha \cdot \beta=-1\end{array}\right.$,
构造方程 $x^2-x-1=0$,
解得 $x_{1,2}=\frac{1 \pm \sqrt{5}}{2}$.
所以:
$$\begin{aligned}& a_n-\frac{1+\sqrt{5}}{2} a_{n-1}=\frac{1-\sqrt{5}}{2}\left(a_{n-1}-\frac{1+\sqrt{5}}{2} a_{n-2}\right) \\& a_n-\frac{1-\sqrt{5}}{2} a_{n-1}=\frac{1+\sqrt{5}}{2}\left(a_{n-1}-\frac{1-\sqrt{5}}{2} a_{n-2}\right)\end{aligned}$$
由(1)、(2)式得:
$$\begin{aligned}& a_n-\frac{1-\sqrt{5}}{2} a_{n-1}=\left(\frac{1+\sqrt{5}}{2}\right)^{n-2}\left(a_2-\frac{1-\sqrt{5}}{2} a_1\right) \\& a_n-\frac{1+\sqrt{5}}{2} a_{n-1}=\left(\frac{1-\sqrt{5}}{2}\right)^{n-2}\left(a_2-\frac{1+\sqrt{5}}{2} a_1\right)\end{aligned}$$
令: $(3) \times \frac{1+\sqrt{5}}{2}-(4) \times \frac{1-\sqrt{5}}{2}$
化简可得:
$$a_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$$
方法四:母函数法。
对于斐波那契数列 $\left\{a_n\right\}$ ,有 $a_1=a_2=1, \quad a_n=a_{n-1}+a_{n-2} \quad(n \geq 2)$
$$\text { 令 } S(x)=a_1 x+a_2 x^2+\cdots+a_n x^n+\cdots$$
那么有:
$$\begin{aligned}& S(x) \cdot\left(1-x-x^2\right) \\= & a_1 x+\left(a_2-a_1\right) x^2+\cdots+\left(a_n-a_{n-1}-a_{n-2}\right) x^n+\cdots \\= & x\end{aligned}$$
因此 $S(x)=\frac{x}{1-x-x^2}$.
不难证明:
$$\begin{aligned}& 1-x-x^2 \\&=-\left(x+\frac{1+\sqrt{5}}{2}\right)\left(x+\frac{1-\sqrt{5}}{2}\right) \\&=\left(1-\frac{1-\sqrt{5}}{2} \cdot x\right)\left(1-\frac{1+\sqrt{5}}{2} \cdot x\right) \\& \text { 因此 } S(x)= \frac{1}{\sqrt{5}}\left[\frac{1}{1-\frac{1+\sqrt{5}}{2} \cdot x}-\frac{1}{1-\frac{1-\sqrt{5}}{2} \cdot x}\right] \\& \text { 再利用展开式 } \frac{1}{1-x}=1+x+x^2+x^3+\cdots+x^n+\cdots\end{aligned}$$
于是就可以得 $S(x)=b_1 x+b_2 x^2+\cdots+b_n x^n+\cdots$
其中 $b_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$
因此可以得到:
$$a_n=b_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]=s^{n-1}+r \cdot s^{n-2}+r^2 \cdot a_{n-2}$$
有趣的是,这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当 $n$ 趋向于无穷大时,前一项与后一项的 比值越来越逼近黄金分割0.618 (或者说后一项与前一项的比值小数部分越来越逼近 0.618)。
$$\begin{aligned}1 \div 1 & =1 \\1 \div 2 & =0.5 \\2 \div 3 & =0.666 \ldots \\3 \div 5 & =0.6 \\5 \div 8 & =0.625 \\& \ldots \\55 \div 89 & =0.617977 \ldots \\144 \div 233 & =0.618025 \ldots \\& \cdots \\46368 \div 75025 & =0.6180339886 \ldots \\& \cdots\end{aligned}$$
越到后面, $\frac{a_n}{a_{n+1}}$ 的比值越接近黄金比。
证明
$$a_a+a_{a+1}=a_{a+2}$$
两边同时除以 $a_{a+1}$ 得到:
$$\frac{a_a}{a_{a+1}}+1=\frac{a_{a+2}}{a_{a+1}} \text {. }$$
若 $\frac{a_n}{a_{n+1}}$ 的极限存在,设其极限为 $x$ ,
则 $\lim _{n \rightarrow \infty} \frac{a_n}{a_{n+1}}=\lim _{n \rightarrow \infty} \frac{a_{n+1}}{a_{n+2}}=x$,
所以 $x+1=\frac{1}{x}$.
由于 $x > 0$,
解得: $x=\frac{\sqrt{5}-1}{2}$.
所以极限是黄金分割比。
平方与前后项
从第二项开始 (构成一个新数列,第一项为 1 ,第二项为 $2 , \ldots \ldots)$ ,每个偶数项的平方都比前后两项之积多 1 ,每个奇数项 的平方都比前后两项之积少1。
如: 第二项 1 的平方比它的前一项 1 和它的后一项 2 的积 2 少 1 ,第三项 2 的平方比它的前一项 1 和它的后一项 3 的积 3 多1。
(注: 奇数项和偶数项是指项数的奇偶,而并不是指数列的数字本身的奇偶,比如从数列第二项 1 开始数,第 4 项 5 是奇 数,但它是偶数项,如果认为 5 是奇数项,那就误解题意,怎么都说不通)
证明经计算可得: $a_n^2-a_{n-1} \cdot a_{n+1}=(-1)^{n-1}$
与集合子集
斐波那契数列的第 $n+2$ 项同时也代表了集合 $\{1,2, \ldots, n\}$ 中所有不包含相邻正整数的子集个数。
奇数项求和
$$a_1+a_3+a_5+a_7+\cdots+a_{2 n-1}=a_{2 n}$$
偶数项求和
$$a_2+a_4+a_6+a_8+\cdots+a_{2 n}=a_{2 n+1}-1$$
平方求和
$$a_1^2+a_2^2+a_3^2+a_4^2+\cdots+a_n^2=a_n \cdot a_{n+1} .$$
隔项关系
$$a_{2 n-2 m-2}\left(a_{2 n}+a_{2 n+2}\right)=a_{2 m+2}+a_{4 n-2 m}, \quad(n > m \geq-1, n \geq 1)$$
两倍项关系
$$\frac{a_{2 n}}{a_n}=a_{n-1}+a_{n+1}$$
其他公式
如果 $a_0=0 , a_1=1 , a_2=1 , a_3=2 , a_4=3 \ldots \ldots$, 则有:
$$\begin{gathered}a_{n-1} \cdot a_{n+1}-a_n^2=(-1)^n . \\\lim _{n \rightarrow \infty} \frac{a_{n-1}}{a_n}=\frac{\sqrt{5}-1}{2} \approx 0.618034\end{gathered}$$
因 $\frac{1}{89} \approx 0.01123 , \frac{1}{9899} \approx 0.000101020305081321$ ,则有:
$$\sum_{n=0}^{\infty} \frac{a_n}{10^{m n+m}}=\frac{1}{10^{2 m}-10^m-1}$$
排列组合
有一段楼梯有 10 级台阶,规定每一步只能跨一级或两级,要登上第 10 级台阶有几种不同的走法?
这就是一个斐波那契数列: 登上第一级台阶有一种登法; 登上两级台阶,有两种登法; 登上三级台阶,有三种登法; 登上四 级台阶,有五种登法.....
$1 , 2 , 3 , 5 , 8 , 13 \ldots \ldots$. 所以,登上十级,有 89 种走法。
类似的,一枚均匀的硬币郑10次,问不连续出现正面的可能情形有:
答案是 $\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{10+2}-\left(\frac{1-\sqrt{5}}{2}\right)^{10+2}\right]=144$ 种。
求递推数列 $a_1=1, \quad a_{n+1}=1+\frac{1}{a_n}$ 的通项公式
由数学归纳法可以得到: $a_n=\frac{F_{n+1}}{F_n}$ ,将斐波那契数列的通项式代入,化简就得结果。
兔子繁殖问题
斐波那契数列又因数学家莱昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死:
我们不妨拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对
两个月后,生下一对小兔对数共有两对
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对
依次类推可以列出下表:
$$\begin{array}{|l|l|l|l|l|l|l|l|l|l|l|l|l|l|}\hline 经过月数 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & \\\hline 幼仔对数 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 & \\\hline 成兔对数 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 & 89 & \ldots \\\hline 总体对数 & 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 & 89 & 144 & \\\hline\end{array}$$
幼仔对数=前月成兔对数
成兔对数=前月成兔对数+前月幼仔对数
总体对数 $=$ 本月成兔对数 + 本月幼仔对数
可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点,那是:前面相邻两项之和,构 成了后一项。
这个数列是中世纪意大利数学家斐波那契在>算盘全书>中提出的,这个级数的通项公式,除了具有 $a(n+2)=a n+a(n+1)$ 的性质 外,还可以证明通项公式为: $a n=(1 / \sqrt{5})^*\left\{[(1+\sqrt{5}) / 2]^{n}-[(1-\sqrt{5}) / 2]^{n}\right\} \quad(n=1,2,3, \ldots)$
数列与矩阵
对于斐波那契数列1、1、2、3、5、8、13、,..。有如下定义
$$\begin{aligned}& F(n)=F(n-1)+F(n-2) \\& F(1)=1 \\& F(2)=1\end{aligned}$$
对于以下矩阵乘法
$$\begin{aligned}& F(n+1)=[11 ] [F(n) F(n-1)]^{T} \\& F(n)=[10 ][F(n) F(n-1) ]^{T}\end{aligned}$$
它的运算就是矩阵[11]乘以矩阵[$F(n) F(n-1)]$ 以及矩阵[10]乘以矩阵$[F(n)F(n-1)],$ 得到:
$$\begin{aligned}& F(n+1)=F(n)+F(n-1) \\& F(n)=F(n)\end{aligned}$$
可见该矩阵的乘法完全符合斐波那契数列的定义
设矩阵A=第一行[11]第二行[10]
迭代n次可以得到: $F(n+1)=A^{n}*[F(2)F(1)]^{\top}=A^{n}*[1,1]$
这就是斐波那契数列的矩阵乘法定义。
另矩阵乘法的一个运算法则 $A^n=A^{\frac{n}{2}} \bullet A^{\frac{n}{2}}(n=2 k, k \in N)$ ,这样我们通过二分的思想,可以实现对数复杂度的矩阵 相乘。
因此可以用递归的方法求得答案。
数列值的另一种求法:
$$F_n=\left[\left(\frac{1+\sqrt{5}}{2}\right)^n\right]$$
其中 $[x]$ 表示取距离 $x$ 最近的整数。
黄金分割
随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割的数值 0.6180339887..…
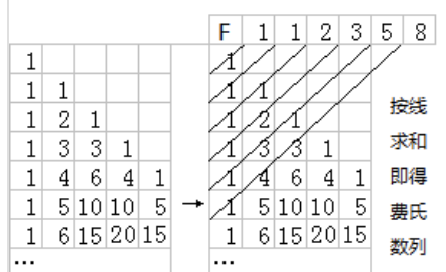
杨辉三角
将杨辉三角左对齐,成所示排列,将同一斜行的数加起来,即得一数列 1、1、2、3、5、8、……
公式表示如下:
$$\begin{aligned}& a_1=\mathrm{C}_0^0=1, \\& a_2=\mathrm{C}_1^0=1, \\& a_3=\mathrm{C}_2^0+\mathrm{C}_1^1=1+1=2, \\& a_4=\mathrm{C}_3^0+\mathrm{C}_2^1=1+2=3, \\& a_5=\mathrm{C}_4^0+\mathrm{C}_3^1+\mathrm{C}_2^2=1+3+1=5, \\& a_6=\mathrm{C}_5^0+\mathrm{C}_4^1+\mathrm{C}_3^2=1+4+3=8, \\& a_7=\mathrm{C}_6^0+\mathrm{C}_5^1+\mathrm{C}_4^2+\mathrm{C}_3^3=1+5+6+1=13, \\& \cdots \\& a_n=\mathrm{C}_{n-1}^0+\mathrm{C}_{n-2}^1+\cdots+\mathrm{C}_{n-1-m}^m \quad(n-1 \geq 2 m)\end{aligned}$$
矩形面积
斐波那契数列与矩形面积的生成相关,由此可以导出一个斐波那契数列的一个性质。
斐波那契数列前几项的平方和可以看做不同大小的正方形,由于斐波那契的递推公 式,它们可以拼成一个大的矩形。这样所有小正方形的面积之和等于大矩形的面积。则可 以得到如下的恒等式:
$$a_1^2+a_2^2+\ldots+a_n^2=a_n \cdot a_{n+1}$$
质数数量
斐波那契数列的整除性与质数生成性
每3个连续的数中有且只有一个被 2 整除,
每4个连续的数中有且只有一个被 3 整除,
每5个连续的数中有且只有一个被 5 整除,
每6个连续的数中有且只有一个被 8 整除,
每7个连续的数中有且只有一个被 13 整除,
每8个连续的数中有且只有一个被 21 整除,
每9个连续的数中有且只有一个被 34 整除,
.......
我们看到第5、7、11、13、17、23位分别是质数:5,13,89,233,1597,28657(第19位不是)
尾数循环
斐波那契数列的个位数:一个60步的循环
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910…
进一步,斐波那契数列的最后两位数是一个300步的循环,最后三位数是一个1500步的循环,最后四位数是一个15000步的循环,最后五位数是一个150000步的循环。
自然界中“巧合”
斐波那契数列在自然科学的其他分支,有许多应用。例如,树木的生长,由于新生的枝条,往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔,例如一年,以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。这个规律,就是生物学上著名的“鲁德维格定律”。
另外,观察延龄草、野玫瑰、南美血根草、大波斯菊、金凤花、耧斗菜、百合花、蝴蝶花的花瓣,可以发现它们花瓣数目具有斐波那契数:3、5、8、13、21……
其中百合花花瓣数目为 3,梅花 5 瓣,飞燕草 8 瓣,万寿菊 13 瓣,向日葵 21 或 34 瓣,雏菊有 34、55 和 89 三个数目的花瓣。
斐波那契螺旋:具有 13 条顺时针旋转和 21 条逆时针旋转的螺旋的蓟的头部
这些植物只是按照自然的规律才进化成这样。这似乎是植物排列种子的“优化方式”,它能使所有种子具有差不多的大小却又疏密得当,不至于在圆心处挤了太多的种子而在圆周处却又稀稀拉拉。叶子的生长方式也是如此,对于许多植物来说,每片叶子从中轴附近生长出来,为了在生长的过程中一直都能最佳地利用空间(要考虑到叶子是一片一片逐渐地生长出来,而不是一下子同时出现的),每片叶子和前一片叶子之间的角度应该是 222.5°,这个角度称为“黄金角度”,因为它和整个圆周 360° 之比是黄金分割数0.618033989……的倒数,而这种生长方式就决定了斐波那契螺旋的产生。向日葵的种子排列形成的斐波那契螺旋有时能达到 89,甚至 144 条。1992 年,两位法国科学家通过对花瓣形成过程的计算机仿真实验,证实了在系统保持最低能量的状态下,花朵会以斐波那契数列长出花瓣。
数字谜题
三角形的三边关系定理和斐波那契数列的一个联系:
现有长为 144 cm 的铁丝,要截成n小段(n≥3),每段的长度不小于 1 cm,如果其中任意三小段都不能拼成三角形,则n的最大值为:
由于形成三角形的充要条件是任何两边之和大于第三边,因此不构成三角形的条件就是存在两边之和不超过另一边。截成的铁丝最小为 1,因此可以放 2 个 1,第三条线段就是 2(为了使得n最大,因此要使剩下来的铁丝尽可能长,因此每一条线段总是前面的相邻2段之和),依次为:1、1、2、3、5、8、13、21、34、55,以上各数之和为 143,与 144 相差 1,因此可以取最后一段为 56,这时 n 达到最大为 10。
我们看到,“每段的长度不小于 1”这个条件起了控制全局的作用,正是这个最小数1 产生了斐波那契数列,如果把 1 换成其他数,递推关系保留了,但这个数列消失了。这里,三角形的三边关系定理和斐波那契数列发生了一个联系。
在这个问题中,这个143是斐波那契数列的前项和,我们是把144超出143的部分加到最后的一个数上去,如果加到其他数上,就有3条线段可以构成三角形了。
卢卡斯数列 1、3、4、7、11、18 ..,也具有斐波那契数列同样的性质。(我们可称之为斐波那契一卢卡斯递推: 从第三项 开始,每一项都等于前两项之和 $\left.a_n=a_{n-1}+a_{n-2} \quad(n \geq 3).\right)$
卢卡斯数列的通项公式为 $a_n=\left(\frac{1+\sqrt{5}}{2}\right)^n+\left(\frac{1-\sqrt{5}}{2}\right)^n$.
这两个数列还有一种特殊的联系 (如下表所示), $a_n \cdot b_n=a_{2 n}$ ,及 $b_n=a_{n+1}+a_{n-1}$.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & \cdots \\\hline 斐波那契数列 F(\mathrm{n}) & 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 & \ldots\\\hline 卢卡斯数列L (\mathrm{n}) & 1 & 3 & 4 & 7 & 11 & 18 & 29 & 47 & 76 & 123 & \cdots \\\hline a_n \cdot b_n & 1 & 3 & 8 & 21 & 55 & 144 & 377 & 987 & 2584 & 6765 & \cdots \\\hline\end{array}$$
类似的数列还有无限多个,我们称之为斐波那契一卢卡斯数列。
如 $1 , 4 , 5 , 9 , 14 , 23 \ldots 因 为 ~ 1 , 4 开 头 , 可 记 作 F[1 , 4]$ ,斐波那契数列就是 $F[1 , 1]$ ,卢卡斯数列就是 $F[1 , 3]$ ,斐波那契 一卢卡斯数列就是 $F[a , b]$ 。
斐波那契—卢卡斯数列之间的广泛联系
①任意两个或两个以上斐波那契—卢卡斯数列之和或差仍然是斐波那契—卢卡斯数列。
②任何一个斐波那契—卢卡斯数列都可以由斐波那契数列的有限项之和获得。