一般地,形如$$y=ax^{2}+bx+c(a,b,c是常数,a\neq0)$$的函数,叫做二次函数。其中$x$是自变量,$a,b,c$分别是函数解析式的二次项系数、一次项系数和常数项。
顶点坐标
$$(-\frac{b}{2a},\frac{4ac-b^{2}}{4a})$$
交点式(仅限于与x轴有交点的抛物线)
$$y=a(x-x_{1})(x-x_{2})$$与x轴的交点坐标是$A(x_{1},0)$和$B(x_{2},0)$。
顶点式
$$y=a(x-h)^2+k$$ 此时顶点为 $(\mathrm{h}, \mathrm{k})$
$k=\frac{4 a c-b^2}{4 a}$ 时,对应顶点为 $(h, k)$ ,其中, $h=-\frac{b}{2 a}$ ;
注意
“变量”不同于“未知数”,不能说“二次函数是指未知数的最高次数为二次的多项式函数”。“未知数”只是一个数(具体值未知,但是只取一个值),“变量”可在一定范围内任意取值。在方程中适用“未知数”的概念(函数方程、微分方程中是未知函数,但不论是未知数还是未知函数,一般都表示一个数或函数——也会遇到特殊情况),但是函数中的字母表示的是变量,意义已经有所不同。从函数的定义也可看出二者的差别
1
二次函数的图像是抛物线,但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图 形。对称轴为直线 $x=-\frac{b}{2 a}$ 。
对称轴与抛物线唯一的交点为抛物线的顶点 $\mathrm{P}$ 。特别地,当 $\mathrm{b}=0$ 时,抛物线的对称轴是 $\mathrm{y}$ 轴 (即直线 $x=0)$ 。
2
抛物线有一个顶点 $\mathrm{P}$ ,坐标为 $\mathrm{P}\left(-\frac{b}{2 a}, \frac{4 a c-b^2}{4 a}\right)$ 。
当 $-\frac{b}{2 a}=0$ 时, $\mathrm{P}$ 在y轴上;
当 $\Delta=b^2-4 a c=0$ 时, $\mathrm{P}$ 在x 轴上。
3
二次项系数 $a$ 决定抛物线的开口方向和大小。
当 $a > 0$ 时,抛物线开口向上;
当 $a < 0$ 时,抛物线开口向下
$|a|$ 越小,则抛物线 的开口越大;
$|a|$ 越大,则抛物线的开口越小 $a b < 0$ ) (可巧记为:左同右异),对称轴在 $y$ 轴右侧。
4
一次项系数$b$和二次项系数$a$共同决定对称轴的位置。当$a$与$b$同号时(即$ab > 0$),对称轴在y轴左侧;
当$a$与$b$异号时(即$ab < 0$)(可巧记为:左同右异),对称轴在y轴右侧。
5
常数项c决定抛物线与 $y$ 轴交点。抛物线与 $\mathrm{y}$ 轴交于 $(0, \mathrm{c})$
6
抛物线与x轴交点个数:
$\Delta=b^2-4 a c > 0$ 时,抛物线与x轴有2个交点。
$\Delta=b^2-4 a c=0$ 时,抛物线与x轴有1个 交点
当 $\Delta=b^2-4 a c < 0$ 时,抛物线与 $\times$ 轴没有交点。
7
当 $a > 0$ 时,函数在$$x=-\frac{b}{2 a}$$处取得最小值 $f\left(-\frac{b}{2 a}\right)=\frac{4 a c-b^2}{4 a}$ ;在 $\left(-\infty,-\frac{b}{2 a}\right]$ 上是减函数,在 $\left[-\frac{b}{2 a},+\infty\right)$ 上是增函数;抛物线的开口向上;函数的值域是 $\left[\frac{4 a c-b^2}{4 a},+\infty\right)$ 。
当 $a < 0$ 时,函数在 $$x=-\frac{b}{2 a}$$处取得最大值 $f\left(-\frac{b}{2 a}\right)=\frac{4 a c-b^2}{4 a}$ ;在 $\left(-\infty,-\frac{b}{2 a}\right]$ 上是增函数,在 $\left[-\frac{b}{2 a},+\infty\right)$ 上是减函数;抛物线的开口向下;函数的值域是 $\left(-\infty, \frac{4 a c-b^2}{4 a}\right]$ 。
当 $b=0$ 时,抛物线的对称轴是 $y$ 轴,这时,函数是偶函数,解析式变形为 $y=a x^2+c(a \neq 0)$ 。
9、值域
当 $\mathrm{a} > 0$ 时,值域是 $\left[\frac{4 a c-b^2}{4 a},+\infty\right)$ ;
当 $\mathrm{a} < 0$ 时,值域是 $\left(-\infty, \frac{4 a c-b^2}{4 a}\right]$ 。
10、奇偶性
当 $b=0$ 时,此函数是偶函数;当 $b$ 不等于0时,此函数是非奇非偶函数。
二次函数的图像都是抛物线,它们的开口向上或向下。一般地,二次函数$$y=ax^{2}+bx+c$$的图像叫做抛物线.
二次函数$y=ax^{2}$的图像和性质如表所示。
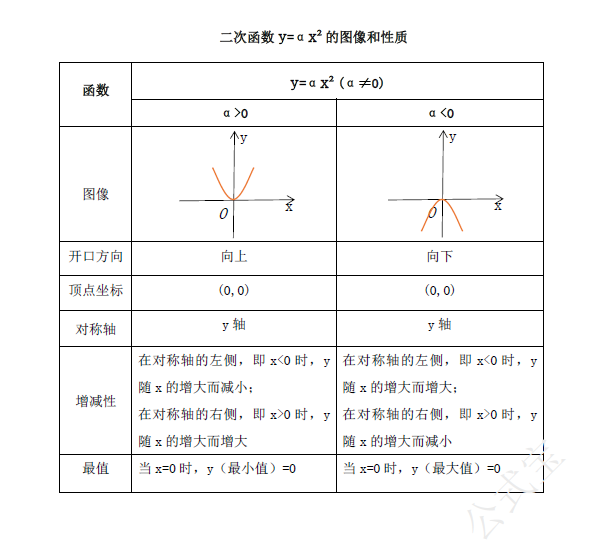
图一 二次函数
与a,b,c有关的代数式符号的判断
在二次函数$y=ax^{2}+bx+c$中,
$a$的正负看抛物线开口方向,开口向上则$a > 0$,开口向下则$a < 0$.
$c$的正负看抛物线与$y$轴的交点的位置。当抛物线与$y$轴相交于正半轴时,$$c> 0.$$当抛物线与$y$轴相交于负半轴时,$$c< 0.$$当抛物线过原点时,$$c=0.$$
$b^{2}-4ac$的正负看抛物线与$x$轴的交点情况
当抛物线与$x$轴有两个公共点时,$$b^{2}-4ac > 0.$$
当抛物线与$x$轴没有公共点时,$$b^{2}-4ac < 0.$$
当抛物线与$x$轴只有一个公共点时,$$b^{2}-4ac=0.$$
$a+b+c$的正负看函数在$x=1$时函数值的情况;$a-b+c$的正负看函数在$x=-1$时函数值的情况。
$4a+2b+c,4a-2b+c$的正负分别看函数在$x=2,x=-2$时函数值的情况。
$2a+b,2a-b$的正负由$-\dfrac{b}{2a}$与1和$-1$的大小决定。
求二次函数的解析式$$y=ax^{2}+bx+c,$$需求出$a,b,c$的值。有已知条件(如二次函数图像上三个点的坐标)列出关于$a,b,c$的方程组,求出$a,b,c$就可以写出二次函数解析式。常用的方法有
常用的设法
一、一般式:$$y=ax^{2}+bx+c(a\neq0);$$
二、顶点式:$$y=a(x-h)^{2}+k(a\neq0),$$其中$(h,k)$为顶点坐标;
三、交点式:$$y=a(x-x_{1})(x-x_{2})(a\neq0),$$其中$x_{1},x_{2}$为抛物线与$x$轴的两个交点的横坐标。
如果抛物线$$y=ax^{2}+bx+c$$与$x$轴公共点,公共点的横坐标是$x_{0}$时,函数值是0,因此$x=x_{0}$是方程$ax^{2}+bx+c=0$的一个根。
二次函数$y=ax^{2}+bx+c$的图像与$x$轴的位置关系有三种:$$\begin{aligned}&没有公共点;\\&有一个公共点;\\&有两个公共点。\end{aligned}$$
这对应着一元二次方程$ax^{2}+bx+c=0$的根有三种情况:$$\begin{aligned}&没有实数根;\\&有两个相等的实数根;\\&有两个不等的实数根。\end{aligned}$$具体如表所示。
若一元二次方程$ax^{2}+bx+c=0$的两根为$x_{1},x_{2}(x_{1}< x_{2})$,则抛物线$y=ax^{2}+bx+c$与$x$轴的交点为$$(x_{1},0),(x_{2},0),$$对称轴为直线$$x=\dfrac{x_{1}+x_{2}}{2}.$$若$a> 0$,当$x < x_{1}$或$x > x_{2}$时,$y> 0;$
当$x_{1}< x< x_{2}$时,$y< 0.$
若$a< 0$,当$x < x_{1}$或$x > x_{2}$时,$y < 0;$
当$x_{1} < x < x_{2}$时,$y > 0.$
如果抛物线$y=ax^{2}+bx+c$与$x$轴交于$M(x_{1},0),N(x_{2},0)$,则$$MN=\dfrac{\sqrt{b^{2}-4ac}}{|a|}.$$
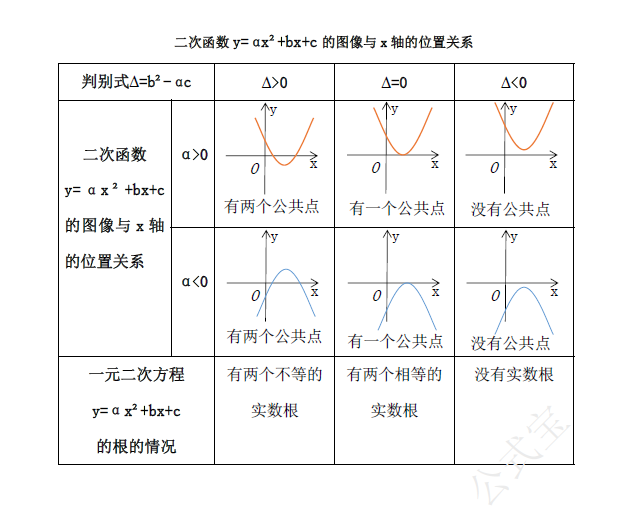
图一 二次函数与一元二次方程的关系










